Physics - Grade XII or Standard XII
Chapter 3: Rotational Motion
Rigid body:
A rigid body is one whose geometric shape and size remains unchanged under the action of any external force.
Axis of rotation:
When a rigid body performs rotation, the particles of the body move in circles. The centres of these circles lie on a straight line called axis of rotation, which is fixed and perpendicular to the planes of circle.
Moment of inertia (I):
M.I. or Moment of inertia or rotational inertia (I) of a rigid body about an axis of rotation is defined as the sum of product of the mass of each particle and the square of its perpendicular distance from the axis of rotation.
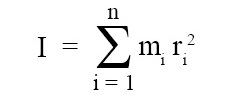
here it is assumed that body consists of ‘n’ particles, m = mass of ith particle, and r = distance of ith particle from the axis of rotation.
Rotational kinetic energy:
Rotational kinetic energy of a rotating body is given by the below given expression:
Erotational = (1/2) I ω2
where, I = moment of inertia, ω = angular velocity.
Click Here to Go To Top of The Page
Angular momentum (L):
Angular momentum of a rotating body is given by the below given expression:
L = I ω
where, I = moment of inertia, ω = angular velocity.
Torque (τ):
To produce rotational motion in a body an unbalanced torque is applied to overcome its inertia. Torque is given by the expression given below:
τ = I α
where, τ = torque, I = moment of inertia, α = angular acceleration. SIU of torque is Nm. Dimensions of torque are same as work.
Click Here to Go To Top of The Page
Analogy between linear motion and rotational motion:
This analogy is shown in the below given table:

Click Here to Go To Top of The Page
Radius of gyration (K):
Radius of gyration of a rotating object is given by the expression given below:
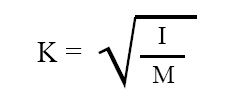
where, K = radius of gyration of object, I = moment of inertia of object, M = mass of object.
Kinetic energy of a body rolling on a plane:
Total kinetic energy of a body rolling on a plane is given by the exprssion given below:
K.E. = Etranslational + Erotational = (1/2) M v2 + (1/2) I ω2
where, M = mass of rolling body, v = speed of center of mass of rolling body, I = moment of inertia of rolling body, ω = angular velocity of rolling body.
Radius of gyration (K) and M.I. (I) of hoop, thin ring, or hollow cylinder:
Radius of gyration and M.I. (moment of inertia) of hoop, thin ring, or hollow cylinder is given by the below given expressions. It is assumed that axis of rotation is same as central axis:
K = R and I = M K2 = M R2
where, K = radius of gyration, R = radius of hoop, thin ring, or hollow cylinder, I = M.I. (moment of inertia) of hoop, thin ring, or hollow cylinder.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of thick ring or annular cylinder:
Radius of gyration and M.I. (moment of inertia) of thick ring or annular cylinder is given by the below given expressions. It is assumed that axis of rotation is same as central axis:
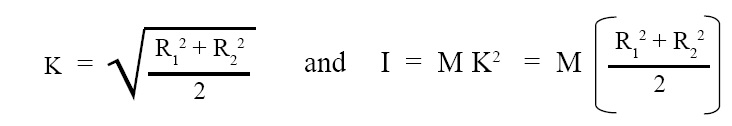
where, K = radius of gyration, R1 = inner radius of thick ring or annular cylinder, R2 = outer radius of thick ring or annular cylinder, I = M.I. (moment of inertia) of thick ring or annular cylinder about its central axis.
Radius of gyration (K) and M.I. (I) of disc or solid cylinder about central axis:
Radius of gyration and M.I. (moment of inertia) of disc or solid cylinder is given by the below given expressions. It is assumed that axis of rotation is same as central axis:
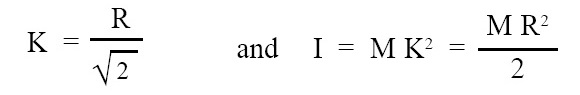
where, K = radius of gyration, R = radius of disc or solid cylinder, I = M.I. (moment of inertia) of disc or solid cylinder about its central axis.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of disc or solid cylinder about central diameter:
Radius of gyration and M.I. (moment of inertia) of disc or solid cylinderabout central diameter, i.e., about transverse axis passing through its centre:
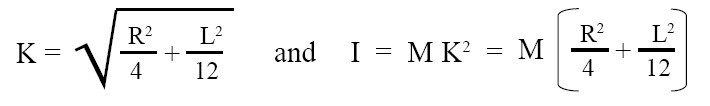
where, K = radius of gyration, R = radius of disc or solid cylinder, L = length of disc or solid cylinder, I = M.I. (moment of inertia) of disc or solid cylinder about its central diameter, i.e., about transverse axis passing through its centre.
Radius of gyration (K) and M.I. (I) of thin rod:
Radius of gyration and M.I. (moment of inertia) of thin rod about an axis passing through its center and perpendicular to its length is given by the below given expressions:
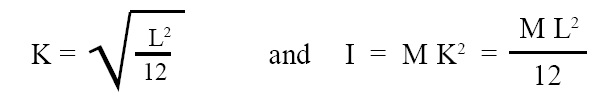
where, K = radius of gyration, L = length of thin rod, I = M.I. (moment of inertia) of thin rod about an axis passing through center and perpendicular to its length.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of thin rod:
Radius of gyration and M.I. (moment of inertia) of thin rod about an axis passing through one of its end points and perpendicular to its length is given by the below given expressions:
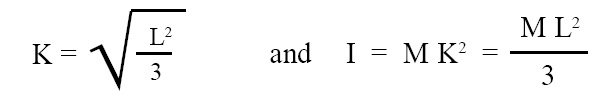
where, K = radius of gyration, L = length of thin rod, I = M.I. (moment of inertia) of thin rod about an axis passing through one of its end points and perpendicular to its length.
Radius of gyration (K) and M.I. (I) of solid sphere:
Radius of gyration and M.I. (moment of inertia) of a solid sphere about any diameter is given by the below given expressions:
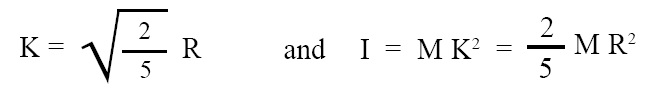
where, K = radius of gyration, R = radius of solid sphere, I = M.I. (moment of inertia) of solid sphere about any diameter.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of a thin spherical shell:
Radius of gyration and M.I. (moment of inertia) of a thin spherical shell about any diameter is given by the below given expressions:
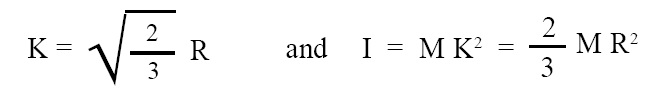
where, K = radius of gyration, R = radius of thin spherical shell, I = M.I. (moment of inertia) of thin spherical shell about any diameter.
Radius of gyration (K) and M.I. (I) of hoop or thin ring about any diameter:
Radius of gyration and M.I. (moment of inertia) of a hoop or thin ring about any diameter is given by the below given expression:
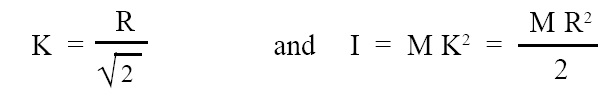
where, K = radius of gyration, R = radius of hoop or thin ring, I = M.I. (moment of inertia) of hoop or thin ring about any diameter.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of hoop or thin ring about a tangent in its plane:
Radius of gyration and M.I. (moment of inertia) of a hoop or thin ring about a tangent in its plane is given by the below given expression:
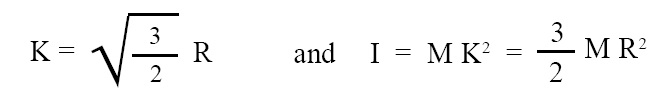
where, K = radius of gyration, R = radius of hoop or thin ring, I = M.I. (moment of inertia) of hoop or thin ring about a tangent in its plane.
Radius of gyration (K) and M.I. (I) of hoop or thin ring about a tangent perpendicular to its plane:
Radius of gyration and M.I. (moment of inertia) of a hoop or thin ring about a tangent perpendicular to its plane is given by the below given expression:
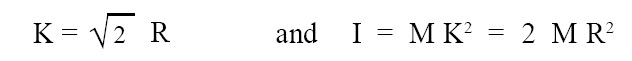
where, K = radius of gyration, R = radius of hoop or thin ring, I = M.I. (moment of inertia) of hoop or thin ring about a tangent perpendicular to its plane.
Click Here to Go To Top of The Page
Radius of gyration (K) and M.I. (I) of a slab:
Radius of gyration and M.I. (moment of inertia) of a slab about an axis passing through its center and perpendicular to its plane is given by the below given expression:
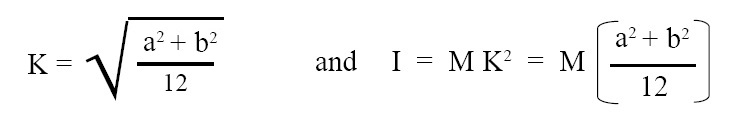
where, K = radius of gyration, a = length of slab, b = width of slab, I = M.I. (moment of inertia) of slab about an axis passing through center and perpendicular to its plane.
Theorem of parallel axes:
This theorem states that moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis passing through its centre of mass and the product of its mass and the square of the perpendicular distance between the two parallel axes. It can be represented in terms of an equation as follows:
Io = Ic + M h2
where, Io = moment of inertia of an object about an axis passing through some point O, Ic = moment of inertia of an object about an axis passing through C which is centre of mass, also, these both axes are parallel to each other, M = mass of object, h = distance between the parallel axes.
Click Here to Go To Top of The Page
Theorem of perpendicular axes:
This theorem states that the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moment of inertia about two mutually perpendicular axes concurrent with perpendicular axis and lying in the plane of the laminar body. It can be represented in terms of an equation as follows:
Iz = Ix + Iy
where, Ix = moment of inertia of a laminar body about X-axis, Iy = moment of inertia of a laminar body about Y-axis, Iz = moment of inertia of a laminar body about Z-axis. It is assumed that X and Y axes are lying in the plane of laminar body. Also, as usual, X, Y, and Z axes are mutually perpendicular.
Click Here to Go To Top of The Page