Periodic motion:

Periodic motion is the motion which repeats itself in equal intervals of time. For example, motion of pendulum of a clock is periodic motion.

Linear S.H.M. (Description):

The motion in which object moves “to and fro” along the straight line is called linear simple harmonic motion or linear S.H.M.

Linear S.H.M. (Definition):

Linear S.H.M. (i.e., linear simple harmonic motion) is defined as the linear periodic motion of a body, in which the restoring force (or acceleration) is always directed towards the mean position and its magnitude is directly proportional to the displacement from the mean position.

Differential equation of linear S.H.M.:

Differential equation of linear S.H.M. is stated below:

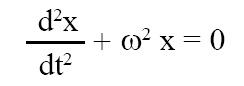
where, m = mass of object performing S.H.M., x = displacement of object from mean position, t = time, ω = angular frequency, also, ω² = k/m, where k = force constant, k/m is always positive, whereas ω may be positive or negative.

Aceleration of S.H.M.:

Acceleration of S.H.M. (means acceleration of object performing S.H.M.) is given by the expression given below:

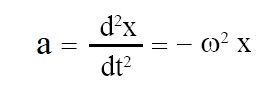
where, a = acceleration of object, x = displacement of object from mean position, t = time, ω = angular frequency.

Velocity in S.H.M.:

Velocity in S.H.M. (means velocity of object performing S.H.M.) is given by the expression given below:

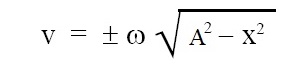
where, v = velocity of S.H.M., i.e., velocity of object performing S.H.M., ω = angular frequency, A = amplitude of S.H.M., x = displacement of object from mean position.

Displacement in S.H.M.:

Displacement in S.H.M. (means displacement of object performing S.H.M.) is given by the expression given below:

x = a sin (ω t + φ)

where, x = displacement of object from mean position, a = amplitude of S.H.M., ω = angular frequency, t = time, φ = phase angle or epoch and its value depends upon initial condition.

Special cases of Displacement in S.H.M.:

Case (a) : If object starts from mean position then x = 0 at t = 0 and expression for displacement in this case is given below:

x = A sin ω t

Case (b) : If object starts from extreme position then x = ± a at t = 0 and expression for displacement in this case is given below:

x = A cos ω t

where, x = displacement of object from mean position, A = amplitude of S.H.M., ω = angular frequency, t = time.

Maximum and minimum displacement in S.H.M.:

Maximum displacement of object performing S.H.M, x_max is ±A and minimum displacement, x_min is 0.

Maximum and minimum velocity in S.H.M.:

Maximum velocity of object performing S.H.M, v_max is ±Aω and minimum velocity, v_min is 0.

Maximum and minimum acceleration in S.H.M.:

Maximum acceleration of object performing S.H.M., a_max is ±Aω² and minimum acceleration, a_min is 0.

Projection of U.C.M.:

Linear S.H.M. is nothing but projection of U.C.M (uniform circular motion) along a diameter of a circle.

Amplitude of S.H.M.:

The magnitude of maximum displacement of the object performing S.H.M. from its mean position or equilibrium position is called amplitude of S.H.M. SIU of amplitude is meter or m. Its direction is away from mean position.

Oscillation:

In S.H.M. the object performs the same set of movement again and again. Such one set of movement is called an oscillation.

Period of S.H.M.:

In S.H.M. the time taken by the object to complete one oscillation is called period of S.H.M. SIU of period is second or s. Expression for period of S.H.M. is given below:

where, T = time period of S.H.M., m = mass of object performing S.H.M., k = force constant.

Frequency of S.H.M.:

The number of oscillations performed by object performing S.H.M. per unit time is called frequency of S.H.M. Expression for frequency is given below:

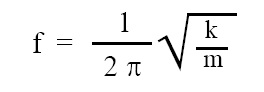
where, f = frequency of S.H.M., m = mass of object performing S.H.M., k = force constant. SIU of frequency is hertz or Hz.

Phase of S.H.M.:

The quantity (ωt + φ) that appears in the expression for displacement of S.H.M. is called phase angle or phase of S.H.M.

Epoch of S.H.M.:

The term φ that appears in the expression for displacement of S.H.M. is called starting phase or initial phase or phase constant or epoch of S.H.M.

Kinetic energy in S.H.M. (KE):

Expression for kinetic energy in S.H.M. is given below:

KE = (1/2) k (A² – x²)

where, KE = kinetic energy in S.H.M., k = force constant, A = amplitude of S.H.M., x = displacement of object from mean position.

Potential energy in S.H.M. (PE):

Expression for potential energy in S.H.M. is given below:

PE = (1/2) m ω² x²

where, PE = potential energy in S.H.M., m = mass of object performing S.H.M, ω = angular frequency of S.H.M., x = displacement of object performing S.H.M. from mean position, k = force constant.

Total energy in S.H.M. (TE):

Total energy in S.H.M. is equal to sum of kinetic energy and potential energy in S.H.M. Expression for total energy in S.H.M. is given below:

TE = KE + PE = (1/2) k A² = (1/2) m ω² A²

where, T.E. = total energy in S.H.M., K.E. = kinetic energy in S.H.M., P.E. = potential energy in S.H.M., k = force constant, A = amplitude of S.H.M., m = mass of object performing S.H.M, ω = angular frequency of S.H.M.

Characteristics of total energy in S.H.M.:

Total energy of object performing S.H.M. is:

(a) directly proportional to its mass,

(b) directly proportional to square of frequency of oscillation, and

(c) directly proportional to square of amplitude of oscillation.

Conversion of energy in S.H.M.:

In S.H.M., total energy is constant but kinetic energy and potential energy are not constant. At mean position total energy = kinetic energy. At extreme position, total energy = potential energy. At other points, total energy is mixture of kinetic energy and potential energy.

Composition of two S.H.M.s having the same period and along the same path:

Let these two S.H.M.s are represented by the below given expressions:

x₁ = A₁ sin (ω t + φ₁)

x₂ = A₂ sin (ω t + φ₂)

here, x1 and x2 are displacements of these two S.H.M.s, A1 and A2 are amplitudes of these two S.H.M.s, and φ₁ and φ₂ are initial phases of these two S.H.M.s. The resultant of these two S.H.M.s is represented by the following expression:

x = R sin (ω t + δ)

thus resultant motion is also S.H.M. whose amplitude is R and intial phase angle is δ. The expressions for R and δ are given below:

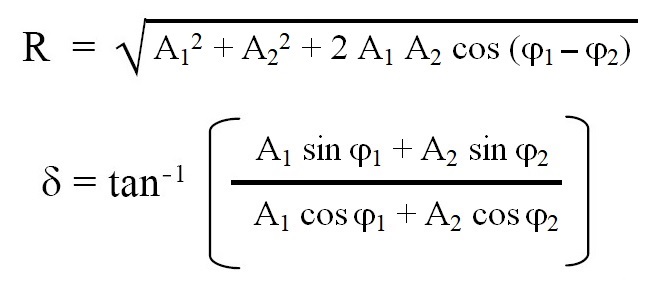
where, R = amplitude of resultant S.H.M., δ = initial phase angle of resultant S.H.M., A1 and A2 = amplitudes of two S.H.M.s, φ₁ and φ₂ = initial phases of two S.H.M.s.

Special cases of composition of two S.H.M.s of same period and along the same path:

Case (a) : If φ₁ = φ₂, then

R = A₁ + A₂

Case (b) If φ₁ – φ₂ = π/2, then

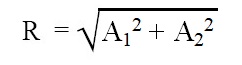
Case (c) : If φ₁ – φ₂ = π, then

R = A₁ – A₂

Case (d) : If φ₁ – φ₂ = 0, and A₁ = A₂ = A, then

R = 2 A

Case (e) : If φ₁ – φ₂ = π/2, and A₁ = A₂ = A, then

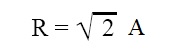
Case (f) : If φ₁ – φ₂ = π, and A₁ = A₂ = A, then

R = 0

Simple pendulum:

An ideal simple pendulum is defined as a heavy particle (point mass) suspended by a weightless, inextensible and twistless string from perfectly rigid support. Practical simple pendulum is defined as a small heavy sphere (bob) suspended by light and inextensible string from a rigid support. The motion of simple pendulum is periodic and oscillatory. If pendulum is displaced through very small angle θ then it performs S.H.M.

Length of simple pendulum:

Length of simple pendulum is defined as the distance between point of suspension and centre of gravity of heavy sphere (bob).

Time period of simple pendulum:

Expression for time period of simple pendulum is given below:

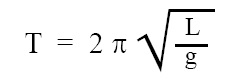
where, T = time period of simple pendulum, L = length of simple pendulum, g = gravitational acceleration due to earth = 9.81 m/s².

Frequency of simple pendulum:

Expression for frequency of simple pendulum is given below:

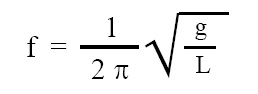
where, T = time period of simple pendulum, L = length of simple pendulum, g = gravitational acceleration due to earth = 9.81 m/s².

Seconds pendulum:

A simple pendulum whose period is 2 second is called seconds pendulum. Length of seconds pendulum is 0.99 m.

Laws of simple pendulum:

Laws of simple pendulum are stated below:

a) Law of length:

The period of simple pendulum is directly proportional to square root of its length.

b) Law of acceleration due to gravity:

The period of simple pendulum is inversely proportional to square root of acceleration due to gravity.

c) Law of mass:

The period of simple pendulum does not depend upon its mass.

d) Law of isochronous:

The period of simple pendulum does not depend upon its amplitude.

Damped oscillations:

When the motion of an oscillator is reduced by an external force, the oscillator and its motion are said to be damped.

Damped harmonic oscillator:

Periodic oscillations of gradually decreasing amplitude are called damped harmonic oscillations and the oscillator is called a damped harmonic oscillator.

Differential equation of damped harmonic oscillations:

Differential equation of damped harmonic oscillations is stated below:

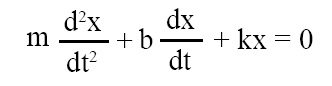
where, m = mass of object performing damped S.H.M., x = displacement of object from mean position, t = time, b = damping constant, k = force constant.

Solution of differential equation of damped S.H.M.:

The solution of differential equation of damped S.H.M. is given below:

x = A e^–bt/2m cos(ω't + φ)

where, A e^–bt/2m = amplitude of damped harmonic oscillations, notice that amplitude decreases with time exponentially. ω’ = angular frequency of damped S.H.M., t = time, φ = phase angle.

Angular frequency and period of oscillation in damped S.H.M.:

Expressions for angular frequency and period of oscillation in damped S.H.M. are given below:

a) Expression for angular frequency:

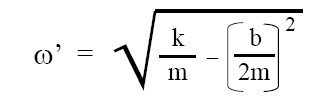
b) Expression for period of oscillation:

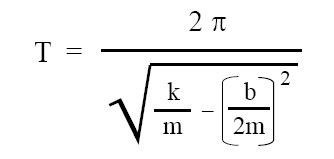
here, ω’ = angular frequency of damped S.H.M., k = force constant, m = mass of object performing damped S.H.M., b = damping constant, T = period of osciallation of damped S.H.M.