Elasticity:

The property by virtue of which material bodies regain their original dimensions (size and shape) after removal of deforming forces is called elasticity.

Elastic bodies:

The bodies which return to their original dimensions (size and shape) after removal of deforming forces are called elastic bodies. Examples: quartz, rubber.

Plasticity:

Plasticity is the property of a material to undergo a permanent deformation even after removal of external deforming forces.

Plastic bodies:

The bodies which do not regain their original dimensions (size, shape, or both) after removal of deforming forces are called plastic bodies. Examples: putty, dough, lead, etc.

Deformation:

The change in size, shape, or both of a body arising due to external forces is called deformation. When deformation of body takes place, the body is said to be in strained condition or deformed state.

Plastic deformation:

The deformation that is irreversible is called plastic deformation. In plastic deformation, body doesn’t return to its original shape and size even after remvoal of external, applied force.

Deforming force:

The force which is responsible for deformation of body is called deforming force. In general, deformation is directly proportional to deforming force.

Stress:

Stress is defined as internal elastic restoring force per unit cross sectional area of body. Alternatively, stress is defined as applied force per unit cross sectional area of body. SIU of stress is N/m² or Pa.

Longitudinal or tensile stress:

When applied force (i.e., deforming force) produces change in length of a body (such as wire, beam, etc.), the stress associated is called longitudinal stress or tensile stress. Let a metal wire of length L and radius r is stretched by a load F, and then it elongates to new length L + dL. Longitudinal or tensile stress in this case is then given by:

Longitudinal or tensile stress = F / A = M g / (π r²)

where, A = area of cross section of wire, M = mass attached to wire, g = gravitational acceleration due to earth, r = radius of wire.

Volume stress:

If a deforming force produces change in volume of a body, the stress associated is called volume stress. Let a block of rubber (with cubical shape) having volume V is subjected to additional pressure dP from all sides, and then its volume decreases to new volume V – dV. Let A be area of its side. Volume stress in this case is then given by:

Volume stress = (applied force) / area = A . dP / A = dP

where, A = area of side of cube, dP = additional pressure applied to sides of cube.

Shearing stress:

If a deforming force produces change in shape of a body, the stress associated is called a shearing stress. Let tangential force F be applied to upper surface of a cube while keeping the lower surface of cube fixed. Now shape of cube changes to parallelopiped. Shearing stress in this case is then given by:

Shearing stress = (tangential applied force) / area = F / A

where, A = area of side of cube, F = tangential applied force.

Strain:

Strain is defined as the change in dimensions per unit original dimension. Strain is a ratio and hence it has no dimention. It is a pure number.

Longitudinal or tensile strain:

If the applied force produces change in length of a body (metal wire, beam, etc.) then strain associated is called longitudinal or tensile strain. Longitudinal or tensile strain is defined as the ratio of change in length to the original length.

Let a metal wire of length L and radius r is stretched by a load F, and then it elongates to new length L + dL. Longitudinal or tensile strain in this case is then given by:

Longitudinal or tensile strain = change in length / original length

Longitudinal or tensile strain = (L + dL - L) / L = dL / L

Volume strain:

If the applied force produces change in volume of body, then strain is called a volume strain. Volume strain is defined as the ratio of change in volume to the original volume.

Let a block of rubber (with cubical shape) having volume V is subjected to additional pressure dP from all sides, and then its volume decreases to new volume V – dV. Volume strain in this case is then given by:

Volume strain = (change in volume) / (original volume)

Volume strain = (V – dV – V) / V = – dV / V

Negative sign indicates that there is decrease in volume with increase in pressure.

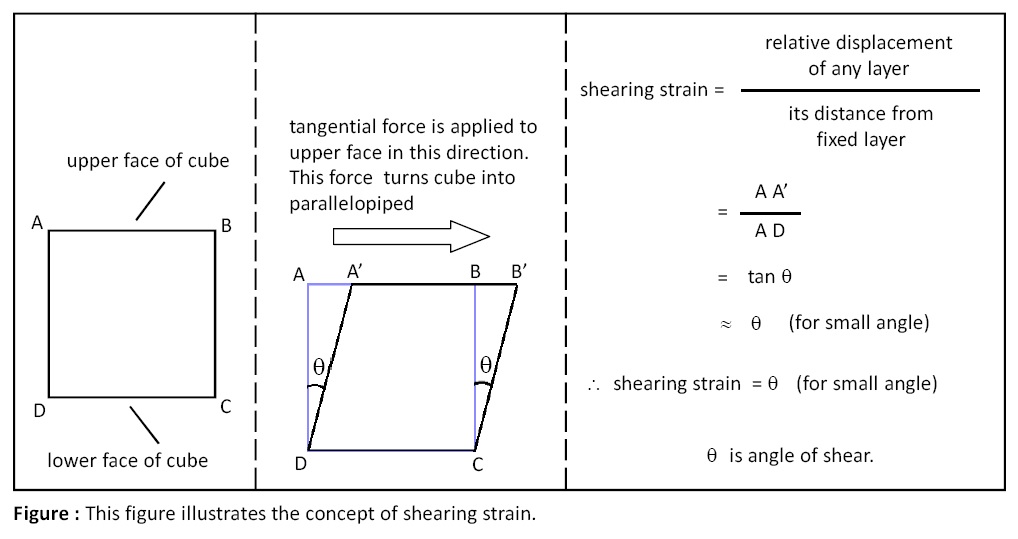
Shearing strain:

If the applied force produces change in shape of a body (cube to parallelopiped) the strain is called shearing strain. Shearing strain is defined as the ratio of relative displacement of any layer to its perpendicular distance from fixed layer. Shearing strain is equal to angle of shear.

Let as illustrated in below given figure, tangential force is applied to lower face of cube while keeping its lower face fixed. This force causes relative displacement of upper layer by distance AA', also cube turns into parallelopiped. Shearing strain in this case is then given by:

Shearing strain = (relative displacement of any layer) / (its distance from fixed layer)

Shearing strain = AA' / AD = tan θ ≈ θ (for small angle)

Hooke’s law:

Hooke’s law states that the deformation of a material is proportional to the force applied to it within elastic limit. Alternatively, Hooke’s law states that within elastic limit, stress is directly proportional to strain.

If we plot a graph of stress (y-axis) Vs strain (x-axis) then we get a straight line and slope of the graph is called modulus of ealsticity.

Modulus of elasticity:

The modulus of elasticity of a material is the ratio of stress to strain. The modulus of elasticity of a material is defined as the slope of stress-strain curve in elastic deformation region. SIU of modulus of elasticity is N/m².

Elastic limit:

The maximum value of stress up to which stress is directly proportional to strain, is called elastic limit.

Permanent deformation:

If stress is applied to body beyond its elastic limit, then body does not return to its original dimensions after removal of the deforming force. This is called permanent deformation or "set."

Young’s modulus (Y or E):

The modulus of elasticity related to change in length of a body (metal wire, beam, etc.) is called Young’s modulus. Young’s modulus is the ratio of longitudinal stress to longitudinal strain. Dimensionally it is equivalent to pressure. Young’s modulus is denoted by letter Y or E. SIU of Young’s modulus is N/m² or Pa.

Let a load Mg be attached to one end of metal wire and other end of metal wire is fixed to ceiling. Let L and r be length and radius of metal wire, respectivly. Let l be extension or elongation in length due to load. Young’s modulus in this case is then given by:

Young’s modulus, Y = (longitudinal stress) / (longitudinal strain)

Young's modulus, Y = (Mg / π r²) / (dL / L)

Bulk modulus (K):

The modulus of elasticity related to change in volume of a body (e.g., rubber cube) is called bulk modulus. Bulk modulus is defined as the ratio of volume stress to volume strain. Dimensionally it is equivalent to pressure. Bulk modulus is denoted by letter K. SIU of bulk modulus is N/m² or Pa.

Let a rubber cube is having volume V. Let additional pressure dP be applied to this cube on all sides. resulting in reduction in its volume from V to V – dV.

Bulk modulus, K = volume stress / volume strain = dP / (dV/V) = V × dP/dV

Compressibility:

The reciprocal of bulk modulus of elasticity is called compressibility of the material. SIU of compressibility is m²/N.

Compressibility = 1 / bulk modulus

Modulus of rigidity (η):

The modulus of elasticity associated with changes in shape of a body is called modulus of rigidity. Modulus of rigidity is defined as the ratio of shearing stress to shearing strain.

Modulus of rigidity, η = shearing stress / shearing strain = (F / A) / θ = F / (A θ)

here, a cube is considered, a tangential force F is applied to upper face of cube while keeping its lower face fixed, let A be area of any face of cube, θ is angle of shear.

Poisson’s ratio (σ):

Within elastic limit, ratio of lateral strain to longitudinal strain is constant and is called Poisson’s ratio.

Poisson’s ratio, σ = lateral strain / longitudinal strain

Elastic limit, yield point, and yield strength:

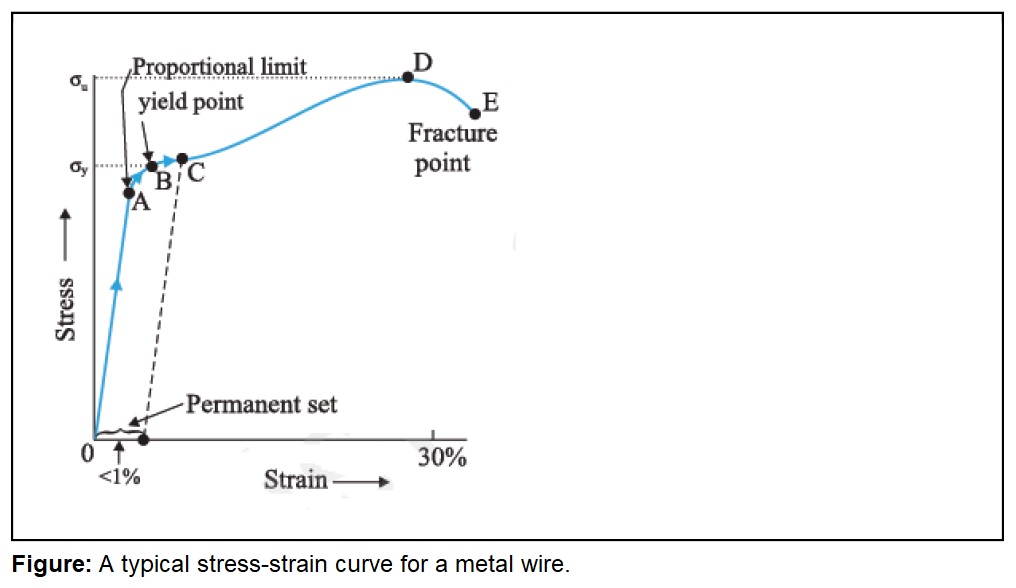
If gradually increasing load is attached to free end of metal wire (other end of metal wire is fixed to ceiling) then it is found that stress is directly proportional to strain upto a particular limit and in the graph (see the below given figure) this limit is shown by point A. Iin this region (i.e., OA) Hooke’s law is obeyed and metal wire behaves as elastic wire. In the region from A to B, stress and strain are not proportional. However, the metal wire still returns to its original dimension when the load is removed. The point B in the curve is known as yield point (or elastic limit) and the corresponding stress is known as yield strength (σ_y) of the material.

Set:

Beyond the point E, we get the curve EE’ (see the figure given above). In this region, the length of wire increases permanently. The strain OS remains permanently in the wire. If the wire is loaded again, we get straight line graph SE’. The strain OS is called set.

Permanent set:

If load is increased further beyond the point B, the stress developed exceeds the yield strength and strain increases rapidly even for a small change in the stress (segment BD of the curve, see the figure given above. When the load is removed in segment BD, the body does not regain its original dimension and the strain is not zero even when the stress is zero. The material is said to have a permanent set.

Plastic deformation:

When material possesses permanent set, it is said to have plastic deformation. Tensile strength : The point D on the graph (see the figure given above) represents the ultimate tensile strength (σ_u) of the material.

Fracture:

Beyond the point D (on the graph shown in the figure given above), additional strain is produced even by a reduced applied force and wire breaks into two pieces at the point E. This phenomenon is called fracture.

Brittle and ductile:

If the points D and E are close (on the graph shown in the figure given above), the material is said to be brittle. If they are far apart, the material is said to be ductile.

Elastomers:

Substances like rubber or tissue of aorta which can be stretched to cause large strains are called elastomers.

Strain energy:

Strain energy is defined as an elastic potential energy gained by a wire during elongation by stretching force. It is given by the following expression:

Strain energy = 0.5 × load × extension

Strain energy per unit volume = (stress)² / (2Y)

where, Y = Young’s modulus.

Buckling:

When a beam supported at both ends is loaded then it is bended. This bending of beam due to load is called buckling.