Physics - Grade XII or Standard XII
Chapter 9: Thermodynamics and
Kinetic Theory of Gases
Modes of heat transfer:
There are three modes of transfer of heat, as follows : (a) conduction, (b) convection, and (c) radiation.
Conduction:
Conduction is the process in which heat is transferred through a material medium, without actual migration of the medium-particles from one place to another.
Convection:
Convection is the process in which, heat is transferred through a material medium, due to the actual migration of the medium-particles from one place to another.
Radiation:
Radiation (also called thermal radiation) is the process in which heat is transferred in the form of electromagnetic waves. Radiation can occur in the absence of any medium. Every body having the temperature greater than 0 K radiates.
Zeroth law of thermodynamics:
According to zeroth law of thermodynamics, if two bodies P and Q are in thermal equilibrium and also the bodies P and R are in thermal equilibrium then bodies Q and R are also in thermal equilibrium.
First law of thermodynamics:
According to first law of thermodynamics, the internal energy Eint of a system tends to increase if energy is added as heat Q and tends to decrease if energy is lost as work W done by the system. This law can be expressed in terms of an equation as follows:
dEint = dQ – dW
where, dEint = increase in internal energy of a system, dQ = addition of heat to system, dW = work done by system.
Click Here to Go To Top of The Page
Second law of thermodynamics:
Mechanical work can be completely converted into heat but heat cannot be completely converted into mechanical work.
Isothermal process:
The process in which temperature of the system is kept constant throughout is called isothermal process. For an isothermal process, the ideal gas equation is:
P V = constant
where, P = pressure of the system, V = volume of the system. This is Boyle’s law.
Adiabatic process:
The process in which system is insulated from the surrounding and no heat transfer takes place between system and surrounding is called adiabatic process. For adiabatic process, the gas equation becomes, as follows:
P Vγ = constant
where, P = pressure of the system, V = volume of the system, γ = Cp / Cv = ratio of specific heats at constant pressure to constant volume, Cp = specific heat of gas at constant pressure, Cv = specific heat of gas at constant volume.
Isobaric process:
The process in which pressure of system is kept constant throughout is called adiabatic process.
Isochoric process:
The process in which volume of system is kept constant throughout is called isochoric process.
Click Here to Go To Top of The Page
Heat engine:
Heat engine is a device that takes heat Q1 from source at higher temperature T1, converts part of it (i.e., Q1 – Q2) to mechanical work and releases remaining heat Q2 to sink at lower temperature T2. Here, T1 > T2.
Efficiency of heat engine (η):
Efficiency of heat engine is given by the below given expression:
η = (Q1 – Q2) / Q1
where, η = efficiency of heat engine, Q1 = heat received by engine from source, Q2 = heat released by engine to sink, T1 = temperature of source, T2 = temperature of sink. Also, T1 > T2.
Refrigerator:
Refrigerator is the reverse of heat engine. Refrigerator is a device that takes heat Q2 from source at lower temperature T2, does some external work W, and releases the heat Q1 = Q2 + W to sink at higher temperature T1. Here, T1 > T2.
Coefficient of performance (COP):
Coefficient of performance (COP) of refrigerator is given by the below given expression:
COP = Q2 / (Q1 - Q2)
where, COP = coefficient of performance of refrigerator, Q2 = heat received by refrigerator from source, Q1 = heat released by engine to sink, T2 = temperature of source, T1 = temperature of sink. Also, T1 > T2.
Click Here to Go To Top of The Page
Absorption, reflection, and transmission of heat radiation:
If Q is the total radiant energy incident upon the surface a body, some part of it Qa will be absorbed, some part Qr be reflected, and some part Qt be transmitted through the body. This can be expressed in terms of equation as follows:
Q = Qa + Qr + Qt
Coefficient of absorption (a):
The coefficient of absorption of a body is defined as the ratio of the quantity of radiant energy absorbed by the body in a given time to the quantity of radiant energy incident on the body in the same time. Coefficient of absorption is also called absorptivity or absorptance:
Coefficient of absorption, a = Qa / Q
Coefficient of reflection (r):
The coefficient of reflection of a body is defined as the ratio of the quantity of radiant energy reflected by the body in a given time to the quantity of radiant energy incident on the body in the same time. Coefficient of reflection is also called reflectivity or reflectance:
Coefficient of reflection, r = Qr / Q
Click Here to Go To Top of The Page
Coefficient of transmission (t):
The coefficient of transmission of a body is defined as the ratio of the quantity of radiant energy transmitted through the body in a given time to the quantity of radiant energy incident on the body in the same time. Coefficient of transmission is also called transmissivity or transmittance:
Coefficient of transmission, t = Qt / Q
where, in the above stated three definitions, Q = quantity of radiant energy incident on the body in a given time, Qa = quantity of radiant energy absorbed by the body in the same time, Qr = quantity of radiant energy reflected by the body in the same time, Qt = quantity of radiant energy transmitted through the body in the same time.
Relation between a, r, and t:
The relation between a, r, and t is given below:
a + r + t = 1
Athermanous substances:
The substances which do not transmit any incident heat radiations (i.e., opaque to heat radiations) are called as athermanous substances.
Examples of athermanous substances:
wood, iron, copper, lampblack, etc. For athermanous substances, a + r = 1 and coefficient of transmission t = 0.
Diathermanous substances:
The substances which are transparent to heat radiations (through which heat radiations can pass) are called as diathermanous substances.
Click Here to Go To Top of The Page
Examples of diathermanous substances:
glass, quartz, sodium chloride, hydrogen, oxygen, dry air, and rock salts.
Perfectly black body:
Perfectly black body is a body which absorbs all the radiant energy (i.e., all radiations of all wavelengths) incident on it. For perfectly black body, coefficient of absorption is one, coefficient of reflection and coefficient of transmission both are equal to zero. Perfectly black body does not exist in nature. However, lampblack absorbs approximately 98% of the radiant heat incident upon it and hence it can be treated as black body.
Wien’s displacement law:
Wien’s displacement law states that the wavelength for which emissive power of blackbody is maximum is inversely proportional to the absolute temperature of the black body. This law is called displacement law because as temperature increases the maximum intensity of radiation emitted by it gets shifted or displaced towards the shorter wavelength side. This law is useful in determining very high temperature of distant stars, moon or celestial bodies. This law can be stated in terms of an equation as follows:
λmax = b / T
where, λmax = wavelength at which radiation from black body is maximum, T = temperature of the black body, b = Wien’s constant = 2.898 × 10-3 mK.
Click Here to Go To Top of The Page
Emissive power (E):
Emissive power ‘E’ of a body at a given temperature is defined as the quantity of radiant energy emitted by the body per unit time per unit surface area of the body at that temperature. It is given in terms of an expression as follows:
E = Q / (At)
where, E = emissive power of a body, Q = radiant energy emitted by the body, A = surface area of the body, t = time for which body radiates energy. SIU of emissive power is J/(m2s) or W/m2.
Coefficient of emission (e):
Coefficient of emission of the body is the ratio of emissive power of the body at a given temperature to the emissive power of a perfectly black body at the same temperature. Coefficent of emission is also called as
emissivity
. Expression for coefficient of emission is given below:Coefficient of emission, e = E / Eb
where, e = coefficient of emission, E = emissive power of an ordinary body at a given temperature, Eb = emissive power of perfectly black body at the same temperature. For perfectly black body, e = 1, for perfect reflector, e = 0, for ordinary bodies, e < 1. Good absorber is good emitter of heat.
Absorptive power:
Absorptive power of a body at a given temperature is defined as the amount of radiant energy absorbed per unit area per unit time by a surface at that temperature.
Click Here to Go To Top of The Page
Kirchhof’s law of radiation:
Kirchhof’s law of radiation states that the coefficient of absorption of a body is equal to its coefficient of emission at any given temperature. This law can be expressed in terms of an equation as follows:
a = e = E / Eb
where, a = coefficient of absorption, e = coefficient of emission, E = emissive power of an ordinary body at a given temperature, Eb = emissive power of perfectly black body at the same temperature.
Stefan’s law of radiation:
Stefan’s law of radiation states that the amount of radiant energy emitted per unit time per unit surface area of perfectly black body is directly proportional to the fourth power of its absolute temperature. Alternatively, Stefan’s law states that the emissive power of a perfectly black body is directly proportional to the fourth power of its absolute temperature. This law can be expressed in terms of an equation as follows:
Eb = σ T4
where, Eb = Q / (At) = emissive power of a black body, σ = Stefan’s constant = 5.67 × 10-8 J/(m2sK4), T = temperature of black body, Q = radiant energy emitted by the black body, A = surface area of the black body, t = time for which black body radiates energy. SIU of emissive power is J/(m2s) or W/m2. Stefan’s constant is also called Stefan-Boltzmann constant.
Click Here to Go To Top of The Page
Net loss of energy by a black body:
If black body having temperature T is placed in surrounding of temperature T0 then net loss of energy by a black body is given by the below given expression:
Enet black body = σ (T4 – T04)
where Enet black body = net loss of energy by a black body per unit area per unit time to surrounding, σ = Stefan's constant = 5.67 × 10-8 J/(m2sK4),T = temperature of the black body, T0 = temperature of the surrounding.
Stefan’s law for ordinary bodies:
Stefan’s law for ordinary bodies can be expressed in terms of an equation as follows:
E = e σ T4
where, E = emissive power of an ordinary body = amount of radiant energy emitted by an ordinary body per unit time per unit area, e = emissivity of that ordinary body, σ = Stefan's constant = 5.67 × 10-8 J/(m2sK4), T = temperature of that ordinary body.
Click Here to Go To Top of The Page
Net loss of energy by ordinary body:
If an ordinary body having temperature T is placed in surrounding of temperature To then net loss of energy by the ordinary body is given by the below given expression:
Enet ordinary body = σ (T4 – T04)
where, Enet ordinary body = net loss of energy by an ordinary body per unit area per unit time to surrouding, e = emissivity of ordinary body, σ = Stefan's constant = 5.67 × 10-8 J/(m2sK4), T = temperature of ordinary body, T0 = temperature of surrounding.
Newton’s law of cooling:
Newton’s law of cooling states that the rate of fall of temperature of a body is directly proportional to (θ – θ0) where θ is the temperature of the body and θ0 is the temperature of the surrounding. Thus:
dθ/dt α (θ – θ0) OR dθ/dt = k (θ – θ0)
where dθ/dt is rate of cooling of the body, dθ is fall in temperture of the body in time dt, and k is the constant of proportionality. This law holds good only for small temperature difference (about 40oC).
Click Here to Go To Top of The Page
Greenhouse effect:
Earth emits thermal radiations. Part of these radiations are absorbed by “greenhouse gases” (i.e., CO2, CH4, etc.) present in atmosphere resulting in heating of atmosphere. This heated atmosphere keeps the earth warm. This warming of earth due to greenhouse gases is known as greenhouse effect. In the absence of greenhouse effect, temperature of earth would have been -18oC. Because of increase in percentage of greenhouse gases, the temperature of earth has been increasing since the past century. If goes unchecked, this warming of earth will result in dire consequences for coming generations.
Assumptions made by kinetic theory of gases:
a) A gas consists of large number of tiny particles called molecules.
b) The molecules are rigid and perfectly elastic spheres of very small diameters.
c) All the molecules of teh same gas are identical in shape, size, and mass.
d) Actual volume occupied by gas molecules is very small and negligible compared to the total volume occupied by the gas.
e) The molecules are always in a state of random motion, i.e., they are moving in all possible directions will all possible velocities. This state is also called as molecular chaos.
Click Here to Go To Top of The Page
f) Due to their random motion the molecules constantly collide with each other and also with the walls of the container. These collisions are perfectly elastic and there is no loss of kinetic energy during the collisions.
g) Between two successive collisions, a molecule travels in a straight line with constant velocity. It is called the free path.
h) The time taken for collision is very small as compared to the time required to cover free path between two successive collisions.
Free path:
The distance travelled by the molecule between two successive collisions is called the free path.
Mean free path:
The average distance travelled by a gas molecule between two successive collisions is known as the mean free path. It can be expressed in terms of an equation as follows:
λ = (λ1 + λ2 + ...... + λN) / N
where λ1, λ2, λN are the free paths, λ = mean free path, N = number of collisions.
Click Here to Go To Top of The Page
Mean velocity or average velocity:
The arithmetic mean of the velocities of individual molecules is called mean velocity or average velocity. It can be expressed in terms of an equation as follows:
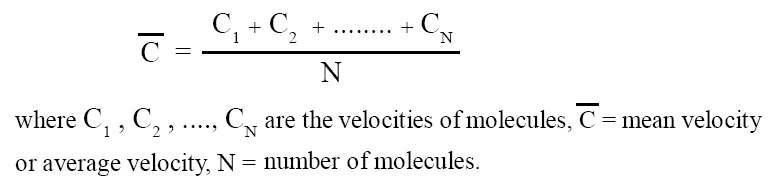
Mean square velocity:
The arithmetic mean of the squares of the velocities of individual molecules is called mean square velocity. It can be expressed in terms of an equation as follows:
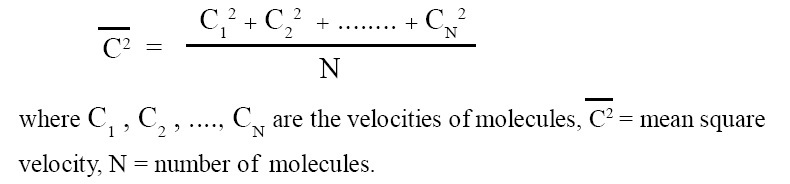
Click Here to Go To Top of The Page
Root mean square velocity:
The square root of mean square velocity is called root mean square velocity. It can be expressed in terms of an equation as follows:
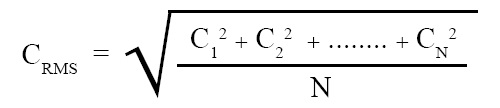
where C1, C2, ...., CN are the velocities of molecules, CRMS = root mean square velocity of the molecules, N = number of molecules.
Formula for pressure of gas:
Formula for pressure of gas derived on the basis of kinetic theory of gases is given below:
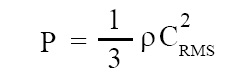
where P = pressure of the gas, ρ = density of gas, CRMS = root mean square velocity of gas molecules.
Click Here to Go To Top of The Page
Formula for root mean square velocity in terms of temperature:
Formula for root mean square velocity in terms of temperature derived on the basis of kinetic theory of gases is given below:
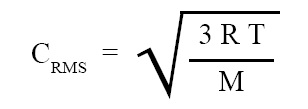
where CRMS = root mean square velocity of the molecules, R = gas constant = 8.31 J/(mol K) , T = temperature of the gas, M = molecular weight of the gas.
Formulae for kinetic energy of gas:
Various formulae for kinetic energy of gas on the basis of kinetic theory of gases are given below:
a) kinetic energy of a gas = (3/2) P V
b) kinetic energy of a gas per unit volume = (3/2) P
c) kinetic energy of a gas per mole or kilomole = (3/2) R T
d) kinetic energy of a gas per molecule = (3/2) kB T
e) kinetic energy of a gas per unit mass = 3 R T / (2 M)
where P = pressure of gas, V = volume of gas, R = gas constant = 8.31 J /(mol K), T = temperature of the gas, kB = Boltzmann’s constant = 1.38 × 10-23 J/K, M = molecular weight of the gas.
Click Here to Go To Top of The Page
Maxwell distribution:
For a given mass of a gas, the velocities of all molecules are not same, even when bulk parameters like pressure, volume, and temperature are fixed. Collisions change the direction and the speed of molecules, but in a state of equilibrium the distribution of speed is constant.
Degrees of freedom:
(a) If a molecule is constrained to move along a line, it requires one co-ordinate to locate it, i.e., it has one degree of freedom, (b) If molecule is constrained to move in a plane, it requires two co-ordinates to locate it, i.e., it has two degrees of freedom, (c) If molecule is allowed to move in space then it requires three co-ordinates to locate it, i.e., it has three degrees of freedom.
Law of equipartition of energy:
In equilibrium, the total energy is equally distributed in all possible energy modes, with each mode having an average energy equal to (1/2) kB T. This is known as law of equipartition of energy.
Specific heat capacities of gases:
Specific heat capacities of gases of various types, computed on the basis of kinetic theory of gases, are given below:
a) Sp. Heat of Monoatomic gases (3 degrees of freedom):
CP = (5/2) R
CV = (3/2) R
γ = CP / CV = 5/3
Click Here to Go To Top of The Page
b) Sp. Heat of Diatomic gases (rigid like dumbbell, 5 degrees of freedom):
CP = (7/2) R
CV = (5/2) R
γ = CP / CV = 7/5
c) Sp. Heat of Diatomic gases (not rigid, 5 degrees of freedom + 1 vibrational mode):
CP = (9/2) R
CV = (7/2) R
γ = CP / CV = 9/7
d) Sp. Heat of Polyatomic gases (3 translational + 3 rotational + f vibrational modes):
CP = (4 + f) R
CV = (3 + f) R
γ = CP / CV = (4 + f) / (3 + f)
Click Here to Go To Top of The Page
e) Sp. Heat of For all gases:
CP – CV = R
where, CP = specific heat of gas at constant pressure, CV = specific heat of gas at constant volume, R = universal gas constant 8.31 J/(mol K), γ = ratio of specific heats of gases.
Specific heat capacity of solids:
Specific heat capacity of solids is given as follows:
C = 3 R
Specific heat capacity of water:
Specific heat capacity of water is as follows (water molecule has three atoms, one oxygen atom and two hydrogen atoms) :
C = 9 R
Click Here to Go To Top of The Page