Friction:

Friction is a property of a surface by virtue of which when one surface slides over another surface there is opposition to the motion. The origin of this opposition can be attributed to following factors:

(a) interlocking between the irregularities on the contact surfaces, and

(b) intermolecular forces of attraction between the two surfaces.

Static friction:

Friction between two bodies in contact, when one body just moves or tends to move over the other is called as static friction.

Kinetic friction:

Friction between two bodies in contact, when one body is sliding over the other is called as kinetic friction (also called, dynamic or sliding friction).

Rolling friction:

Friction between two bodies in contact, when one body is rolling over the other is called as rolling friction.

Notice that static friction > kinetic friction > rolling friction.

Coefficient of static friction (μ_s):

Coefficient of static friction (μ_s) is defined as the ratio of limiting force of static friction (F_s) to normal reaction (N) between the two surfaces in contact.

Coefficient of kinetic friction (μ_k):

Coefficient of kinetic friction (μ_k) is defined as the ratio of limiting force of kinetic friction (F_k) to normal reaction (N) between the two surfaces in contact.

Fluid:

Fluid is a substance that can flow. Thus liquids and gases are fluids.

Pressure:

Pressure is defined as force per unit area (pressure = force / area). S I Unit of pressure is pascal (Pa). CGS unit of pressure is dyne/cm². Pressure is a scalar quantity.

Notice, 1 N/m² = 1 pascal = 1 Pa

Pressure due to liquid column:

Pressure due to liquid column is given by the expression:

P = ρ . h .g

where P = pressure due to liquid column (in Pa), h = height of liquid column (in m), ρ = density of liquid (in kg/m³), g = gravitational acceleration due to earth = 9.81 m/s².

Hydrostatic paradox:

The shape of the vessel containing the liquid does not affect the pressure. This is known as Hydrostatic paradox.

Pascal’s law:

The pressure applied to any part of the enclosed fluid at rest is transmitted undimin- ished to every portion of the fluid and to the walls of the vessel.

Applications of Pascal’s law:

Applications of Pascal’s law are : (a) hydraulic press, (b) hydraulic lift, (c) hydraulic brakes.

Viscocity:

The property of fluid by virtue of which it opposes the relative motion between its layers is called viscocity.

Streamline or steady or laminar flow:

If velocity of the moving fluid at any fixed point does not change with time then this flow is called streamline or steady or laminar flow.

Turbulent or nonsteady or nonlaminar flow:

If velocity of the moving fluid at any fixed point changes with time then this flow is called turbulent or nonsteady or nonlaminar flow.

Critical velocity (v_c):

It is a particular limiting value of velociy of moving fluid above which the flow of fluid is turbulent (or nonsteady or nonlaminar) and below which the flow of fluid is streamline (or steady or laminar).

Viscous force:

The tangential force acts on adjecent layer of fluid, which opposes the relative motion between the layers of the liquid or gases, is called viscous force or viscous drag.

Velocity gradient:

The rate of change of velocity with distance measured from stationary layer is called velocity gradient. Let v and v + dv be the velocity of layers of liquid which are at distance of x and x + dx respectively from the bottom, therefore:

Velocity gradient = dv / dx

Newton’s law of viscocity:

For streamline flow, viscous force acting on any layer is directly proportional to (i) area of layer, and (ii) velocity gradient.

Let A be the area of layer and dv/dx be the velocity gradient, then viscous force F is proportional to product of A and dv/dx (symbol α means "is proportional to"):

F α A . (dv/dx)

∴ F = η . A . (dv/dx) (η is constant of proportionality)

η = F / [A . (dv/dx)]

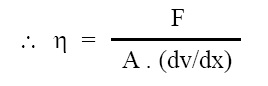
where η is coefficient of viscocity. Its SIU is N.s/m² and CGS unit is dyne.s/cm² or poise. Relation between SI and CGS unit of η is as follows:

1 N.s/m² = 10 poise

Coefficient of viscocity (η):

The coefficient of viscocity (η) is defined as the viscous force per unit area per unit velocity gradient.

Notice, coefficient of viscocity (η) is that parameter which gives some idea about viscociy of fluid. More the viscous fluid larger the value of coefficient of viscocity (η).

Stoke’s law:

According to Stoke’s law, the viscous force F acting on a small sphere falling through a fluid is directly proportional to the radius r of the sphere, its velocity v through fluid, and coefficient of viscocity (η) of fluid is given by the expression:

F = 6 π r η v

Terminal velocity:

A spherical body dropped in a viscous fluid, after traversing some distance, attains a constant velocity called terminal velocity. At terminal velocity, total downward force (gravitaitonal force) is balanced by total upward force (viscous force + buoyancy or upthrust force).

Expression for coefficient of viscocity (η):

Expression for coefficient of viscocity (η) based on Stoke’s law is as follows:

η = (2/9) × (r² (ρ - σ) g / v)

where r = radius of solid spherical body falling through fluid, v = terminal velocity of spherical body, r = radius of spherical body, ρ = density of material of solid spherical body, σ = density of fluid, g = gravitational accleration due to earth 9.81 m/s².

Reynold’s number (Re):

Reynold’s number (Re) is given by the following expression:

Re = v_c . ρ . D / η

where Re = Reynold’s number, v_c = critical velocity, ρ = density of liquid, D = diameter of tube, η = coefficient of viscocity. Reynold’s number is a pure number, it has no unit. Above expression can also be used to define critical velocity as v_c = Re . η / (ρ . D).

Significance of Reynold’s number (Re):

(a) If Re lies between 0 to 2000 then flow of liquid is laminar (steady), (b) If Re lies between 2000 to 3000 then flow is partly laminar and partly turbulent, (c) If Re is greater than 3000 then flow of liquid is turbulent.

Bernoulli’s principle:

In case of the streamline flow of non-viscous and incompressible fluid, the sum of (a) pressure energy, (b) kinetic energy per unit mass, and (c) potential energy per unit mass always remains constant at every point. This principle can be stated in the form of expression as follows:

P + (1/2) ρ v² + g h

In the LHS of above equation, first term (P) denotes pressure energy, second term ((1/2) ρ v²) denotes K.E. per unit mass, and third term (g h) denotes P.E. per unit mass. In this equation, P = pressure energy, p = density of fluid, v = velocity of fluid, g = gravitational acceleration due to earth = 9.81 m/s², h = height of fluid from the ground or lowest reference level.

Toricelli’s law:

This law is nothing but an expression that gives speed of efflux as follows:

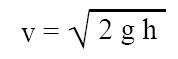
where v = speed of efflux (fluid coming out through orifice), g = gravitational acceleration due to earth, h = height of surface of fluid from orifice.

Applications of Bernoulli’s principle:

(a) venturi-meter, it is a device that measures speed of incompressible fluid, (b) design of aircraft wing, (c) bunsen burner, and (d) air purifier.