Periodic motion:

A motion that repeats itself in equal intervals of time is called a periodic motion.

Oscillatory or vibrating motion:

If an object makes to and fro motion about its mean or equilibrium position then then this motion is called oscillatory or vibrating motion.

Oscillator or vibrator:

If an object is performing oscillatory or vibrating motion that object is called oscillator or vibrator.

Oscillation:

An oscillating object makes to and fro movement. One complete set of to and fro movement is called an oscillation.

Period or time period of oscillation (T):

Time taken by the object to complete one oscillation is called period or time period of oscillation (T).

Frequency of oscillation (n or ν):

The number of oscillations performed by the oscillating object per second is called frequency of oscillation.

Amplitude of oscillation (A):

The maximum displacement of the oscillating object from its mean position is called amplitude of oscillation.

Damped oscillations:

Oscillations of object are opposed by resistive forces due to medium. The oscillator has to spend some energy and the amplitude of vibration goes on decreasing and finally becomes zero. Such oscillations are called damped oscillations.

Wave motion:

Wave motion is propagation of disturbance (energy) through the medium in terms of oscillations of particles of medium.

Elastic waves or mechanical waves:

Waves which require material medium for their propagation are called mechanical waves.

Properties of medium:

Propagation of elastic or mechanical waves is possible through a medium provided that medium possesses the following properties:

(a) medium should be continuous and elastic, i.e., medium should regain original state after removal of deforming force,

(b) medium should possess inertia, i.e., it must be capable of storing energy and transfer it in the form of waves, and

(c) the frictional resistance of medium must be negligible so that there will be no damped oscillations.

Progressive waves:

Waves which travel continuously in the same direction in the given medium without change of form are called progressive waves. Progressive waves are classified as transverse waves and longitudinal waves.

Characteristics of Progressive Waves:

(i) all the vibrating particles of medium have same ampli- tude, period, and frequency, (ii) state of oscillation changes from particle to particle, (iii) progressive waves transfer energy through the medium.

Transverse wave:

A wave in which particles of medium vibrate in a direction perpendicular to the direction of propagation of the wave is called transverse wave. Waves on the surface of water are transverse waves.

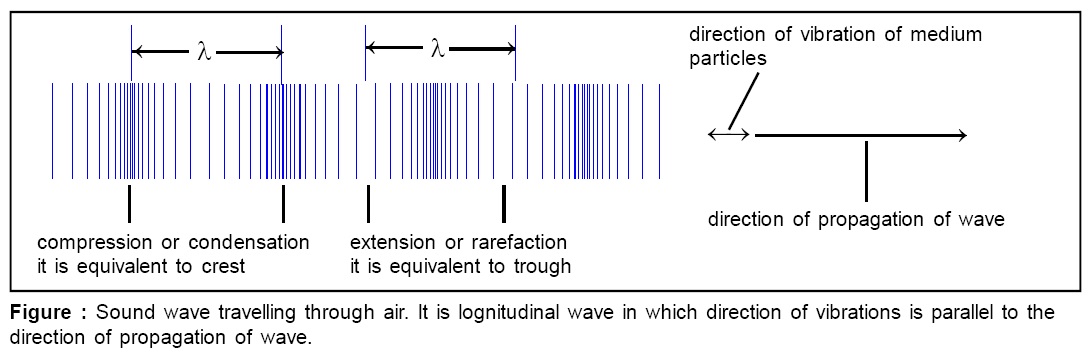
Electromagnetic waves (e.g., light) are also transverse waves but don’t need medium for propagation. Longitudinal wave : A wave in which particles of medium vibrate in a direction parallel to the direction of propagation of the wave is called longitudinal wave. Sound waves are longitudinal waves.

Velocity of wave:

Velocity of wave (transverse or longitudinal) is given by the following expression:

v = ν . λ OR v = n . λ

where v = velocity of wave, ν or n = frequency of wave, and λ = wavelength or wave.

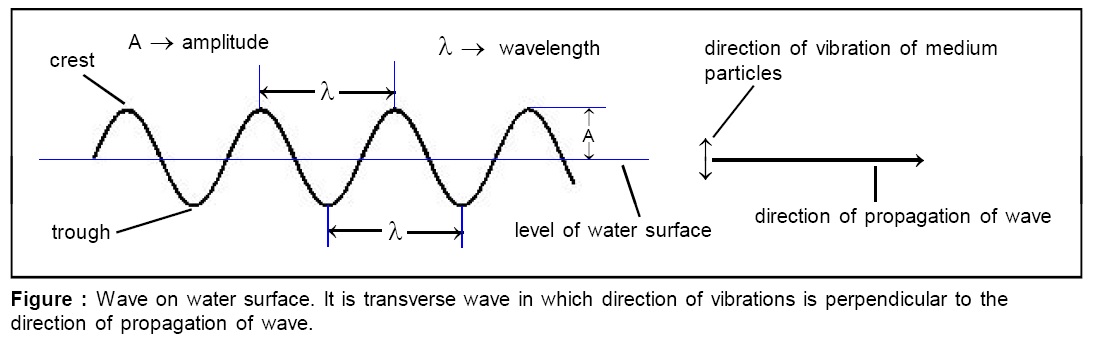
Wavelength of wave (λ):

The distance between two successive crests or troughs (in case of transverse waves) or distance between two successive compressions or rarefactions (in case of longitudinal waves) is called wavelength of wave. It is denoted by letter λ.

Time period of wave (T):

The time required by wave to travel the distance equal to its wavelength is called time period of wave.

Frequency of wave (ν or n):

The frequency of wave (ν or n) is given by the following expression:

ν (or n) = 1 / T where T = time period of wave.

Characteristics of transverse waves:

(i) medium particles vibrate in a direction that is perpendicular to the direction of propagation of wave,

(ii) during propagation of wave medium is divided in into alternate crests and troughs,

(iii) the distance between any two successive crests or troughs gives us wavelength of wave and it is denoted by letter λ,

(iv) crests and troughs advance in the medium and are responsible for transfer of energy,

(v) when transverse waves propagate through medium there is no change of pressure or density anywhere in the medium,

(vi) speed of transverse wave travelling along a stretched string is given by:

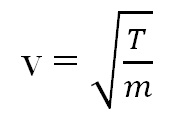
where v = speed of wave on string, T = tension in the string and m = mass per unit length of string,

(vii) transverse waves can be polarized. For example, sunlight can be polarised.

Characteristics of longitudinal waves:

(i) medium particles vibrate in a direction that is parallel to the direction of propagation of wave,

(ii) during propagation of wave, medium is divided into alternate compressions and rarefactions,

(iii) the distance between any two successive compressions or rarefactions gives us wavelength of wave and it is denoted by letter λ,

(iv) for successful propagation of wave, medium should possess the property of elasticity of volume, and hence, longitudinal waves travel through solids, liquids, and gases,

(v) compressions and rarefactions advance in the medium and are responsible for the transfer of energy,

(vi) during propagation of wave, there is variation in pressure and density along the path of wave,

(vii) the velocity of longitudinal wave travelling through medium is given by:

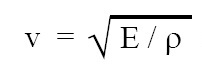
where E = modulus of elasticity of the medium and ρ is the density of medium, (viii) longitudinal waves cannot be polarised.

Newton’s formula for velocity of sound:

Newton obtained the formula for velocity of sound as given below:

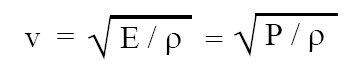
where v = velocity of sound, E = modulus of elasticity of air, ρ = density of air, P = atmospheric pressure. Newton erroneously assumed that propagation of sound wave through air is an isothermal process (actually it is adiabatic process). If this propagation is isothermal then E = P. The velocity computed using this formula turns out to be 279.9 m/s, whereas the actual velocity of sound in air is 332 m/s.

Laplace’s correction to Newton’s formula:

Newton thought that heat developed during com- pression and cooling during rarefaction finds sufficient time for its dissipation and hence the tem- perature of medium remains constant. Thus propagation of sound wave is isothermal process. Laplace pointed out that formation of compression and rarefaction take place so quickly that its dissipation is not possible. Consequently, the propagation of sound wave is not isothermal but adiabatic process, and hence, E = γ. P where γ = c_p / c_v = 1.4, also, c_p = specific heat of air at constant pressure, c_v = specific heat of air at constant volume. Thus Laplace’s formula turns out to be, as follows:

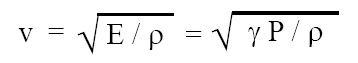
now putting the suitable values in the above expression, the velocity of sound turns out to be 332.3 m/s which is in close agreement with experimental values.

Effect of pressure on the velocity of sound:

For a gaseous medium obeying ideal gas equation, change in pressure has no effect on velocity of sound unless it is accompanied by change in temperature.

Effect of temperature on the velocity of sound:

Effect of temperature on the velocity of sound is in accordance with the expression given below:

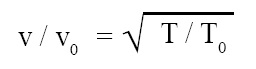
where v = velocity of sound at temperature t^oC, v₀ = velocity of sound at temperature 0^oC, T = absolute temperature (temperature in Kelvin) corresponding to temperature t^oC, T₀ = absolute temperature (temperature in Kelvin) corresponding to temperature 0^oC.

Effect of humidity on the velocity of sound:

Effect of humidity on the velocity of sound is in accordance with the expression given below:

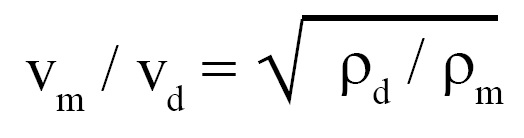
where v_m = velocity of sound in moist air, v_d = velocity of sound in dry air, ρ_d = density of dry air, ρ_m = density of moist air.

Energy of a vibrating particle (or object):

Energy of a vibrating particle (or object) is given by the following exprssion:

E = k A² n²

where E = energy of vibrating particle, A = amplitude of vibration, n = frequency of vibration, k = constant of proportionality.

Musical sound:

Sound produced by musical instruments (e.g., flute, violin, etc.) has pleasant effect on listener is called musical sound. Musical sounds are due to periodic vibrations.

Noise:

Sound produced by shouting of person, thunder storm, etc. has unpleasant effect on listener is called noise. Noises are due to irregular vibrations.

Note:

A sound due to pure sine vibration is called a note.

Characteristics of musical sound:

Two musical sounds differ from one another in three ways: loudness, pitch, and quality or timbre.

Loudness:

Loudness is the characteristic by virtue of which we distinguish two sounds of same frequency. More the intensity of vibration, more the loudness. More the loudness, more the ampli- tude of sound wave.

Pitch:

Pitch of note is the frequency of vibrations of the source. When pitch is high, sound is said to be shrill (e.g., women’s voice). When pitch is low, sound is said to be flat (e.g,, men’s voice).

Quality or timbre:

It is the characteristic that distinguishes two sounds of same pitch and loudness. Musical sound has good quality or timbre, it consists of a series of tones of different frequencies called overtones.

Fundamental tone:

Tone of smallest frequency is called the fundamental tone.

Harmonics:

In musical instruments, the fundamental tone and series of overtones having frequencies in the ratio of 1 : 2 : 3 etc. are present. Such series of tones is called the harmonics.

Conchord or consonance:

When two notes produce pleasant sesnation in the ear, there is conchord or consonance. These notes are called consonant notes.

Dischord or dissonance:

When two notes produce unpleasant sensation in the ear, there is dischord or dissonance. These notes are called dissonant notes.

Harmony:

When two or more notes are sounded together, they produce a pleasant effect due to conchord called harmony.