Frictional electricity:

The electricity developed in objects, when they are rubbed with each other, is called frictional electricity.

Principle of conservation of electric charges:

Electric charge can neither be created nor be de- stroyed but it can be transferred from one part of a system (substance) to other part of the system, so that total charge of an isolated system should remain constant. There are two types of charges: positive and negative. SIU of electric charge is coulomb or C.

Coulomb’s law of electrostatics:

Two electrically charged particles, namely 1 and 2, separated by distance r experience an attractive or repulsive force. Force is attractive between unlike charges (one particle positive and another particle negative) and repulsive between like charges (both particles positive or both particles negative). The magnitude of force between the particles 1 and 2, placed in vacuum, is given by:

F = k_Coulomb × q1 × q2 / r²

where F = electrostatic force between the particles 1 and 2, q1 and q2 = electric charges on particles 1 and 2, r = distance between the particles 1 and 2. The force acts along the line joining the two particles, k_Coulomb = Coulomb's constant = 8.99 × 10⁹ N.m²/C²

Instead of vacuum, if charges are placed in medium of dielectric constant k_dielectric then Coulomb’s law becomes as follows:

F = (k_Coulomb / k_dielectric) × q1 × q2 / r²

where k_dielectric = dielectric constant of the medium.

Coulomb’s law in vector form:

The force exerted by particle 1 on particle 2 (assuming like charges) is as follows (bold letters denote vectors):

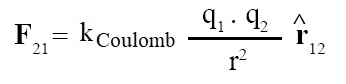
where ^r₁₂ = unit vector directed from particle 1 to particle 2. Forces on both particles are opposite and along the line joining the particles. F21 = –F12.

Dielectric constant (k):

The ratio of the permittivity of the medium to the permittivity of vacuum is called dielectric constant ( k ) of the medium. Dielectric constant (k) is also defined as relative permittivity of the medium with respect to vacuum.

Force between multiple electric charges and principle of superposition of forces:

When there are number of charges situated then force on any one charge can be found using the superposition principle of forces. According to this principle : when a number of charges are interacting, the total force on a given charge is the vector sum of individual forces exerted on the given charge by all other charges.

Suppose there are charges q₁, q₂, ......, q_n situated in free space randomly. If F₁₂, F₁₃, ......, F_1n be the forces exerted on charge q₁ due to charges q₂, q₃, ......, q_n respectively. Then according to principle of superposition of charges the resultant force F₁ experienced by charge q₁ is given by:

F₁ = F₁₂ + F₁₃ + ......+ F_1n

Linear charge density (λ):

Charge per unit length of conductor is called linear charge density (λ). If q is the charge distributed uniformly over a thin conductor of length L, then its linear charge density λ is given by :

λ = q / L

SIU of linear charge density is C/m or coulomb/metre.

Surface charge density (σ):

When the charge is distributed uniformly over an area in space, then charge per unit area is called surface charge density (σ). If q is the charge distributed uniformly over the area A in space, then surface charge density σ is given by:

σ = q / A

SIU of surface charge density σ is C/m² or coulomb/metre².

Volume charge density (ρ):

When the charge is distributed uniformly within a volume, then charge per unit volume is called volume charge density (ρ). If q is the charge distributed uniformly within the volume V, then surface charge density ρ is given by:

ρ = q / V

SIU of volume charge density ρ is C/m³ or coulomb/metre³.

Electric field:

The space surrounding an electric charge, in which any other electric charge experiences a force is called electric field of the charge.

Electric field intensity (E):

The electric field intensity due to a point charge at any point in the electric field is defined as the electrostatic force exerted by it on a unit positive charge placed at that point. Let a positive test electric charge q is placed at a point in an electric field and let this test charge experiences a force F then electric field E at that point is given by :

E = F / q

Electric field intensity E is a vector quantity and its direction is same as that of F. SIU of electric field intensity E is N/C or V/m (i.e., newton / coulomb or volt / metre).

Expression for electric field intensity (E) due to a point charge:

Expression for electric field intensity E at point P due to a point charge q is given by (bold letters denote vectors) :

where r^ = unit vector directed along E or r, r is a radius vector drawn from charge q to point P, and k_Coulomb = Coulomb's constant = 8.99 × 10⁹ N.m²/C²

Line of force:

Line of force (also called, electric line of force) is used to represent electric field graphically. The path along which a unit positive charge moves is called a a line of force. The line of force is defined as a line (straight or curved) such that the tangent at any point to this line gives the direction of the electric field at that point.

Properties of lines of force:

(a) a line of force begins from a positive charge and ends at a negative charge,

(b) lines of force never cross or meet each other,

(c) magnitude of electric field intensity in any region is proportional to number of lines of force per unit area in that region, and

(d) in uniform electric field, lines of force are parallel to each other.

Uniform electric field:

When direction of electic field intensity E is same at all points in the electric field then it is called uniform electric field.

Non uniform electric field:

When direction of electric field intensity E is random at different points in electric field then it is called non uniform electric field.

Radial electric field:

When direction of electric field is radial then it is called radial electric field.

Electric dipole:

Two equal and opposite electric charges (say, +q and –q) separated by a finite distance (say, 2.l) form an electric dipole.

Axis of dipole:

A line passing through the centres of two charges forming an electric dipole is called axis of dipole.

Equator of dipole:

A straight line drawn perpendicular to the axis and passing through centre of electric dipole is called equator of dipole.

Electric dipole moment (p):

The product of magnitude of one of the charges (i.e., q) of dipole and the distance between the two charges (i.e., 2.l) is called electric dipole moment (p). Thus,

p = q × 2.l

where p = dipole moment, q = magnitude of one of the charges, and 2.l = distance between two charges. Dipole moment p is a vector quantity and its direction is from negative charge to positive charge. SIU of dipole moment is C.m or coulomb.metre.

Couple acting on an electric dipole in uniform electric field:

Couple acting on an electric dipole in uniform electric field is given by the following expression (this is cross product of vectors p and E):

τ = p × E

where τ = torque acting on dipole, p = dipole moment, E = electric field. Here, τ, p and E are vector quantities. The cross product of vectors p and E gives us τ.

Electrostatic potential energy:

The electrostatic potential energy of a system of point charges is defined as the work required to assemble the system of charges by bringing them from infinity to their present locations.

Electric potential (V) due to a point charge:

Electric potential (V) at a point in electric field is defined as the amount of work done to bring a unit positive charge from infinity to that point against the direction of electric intensity. SIU of electric potential is volt or V. Also,

1 V = 1 J/C

Expression for the electric potential (V) due to a point charge:

The expression for the electric potential V at point P due to a point charge q is given below:

V = k_Coulomb × q / r

where, k_Coulomb = Coulomb's constant = 8.99 × 10⁹ N.m²/C², q = charge, r = distance between charge q and point P.

Relation between electric field intensity and electric potential:

The relation between electric field intensity and electric potential is given by the following expression:

E = – dV/dx

where dV/dx = rate of change of electric potential with respect to distance = potential gradient, negative sign in this expression shows that electric potential decreases with distance measured in the direction of electric field E.

Electric potential due to an electric dipole:

The electric potential at point P due to an electric dipole is given by the following expression :

V = k_Coulomb p cosθ / r²

where p = dipole moment, r = OP = distance between point P and center of dipole O, θ = angle betwen axis of dipole and OP. If point P is on axis of dipole (but not at the center of dipole) then θ = 0^o and cosθ = 1, also, if point P lies at the center of dipole then V = 0; also, if point P lies on equator of dipole then θ = 90^o, and cosθ = 0, and hence V = 0.

Electric potential due to a system of charges:

The electric potential at point P due to a system of charges q₁, q₂, ......, q_N is can be computed using a principle of superposition. Let these charges are situated from point P at distances r₁, r₂, ......, r_N respectively. Let electric potential at P due to these individual charges be V₁, V₂, ......, V_N. The resultant electric potential V at P due these charges is given by the following expression :

V = V₁ + V₂ + ...... + V_N

V = k_Coulomb [(q₁ / r₁) + (q₂ / r₂) + ...... + (q_N / r_N)]

where, k_Coulomb = Coulomb's constant = 8.99 × 10⁹ N.m²/C².

Equipotential surface:

A surface with constant value of electric potential at all points on it is called an equipotential surface. Equipotential surfaces of a single point charge are concentric spherical surfaces centered at charge. For uniform electric field E, say along X-axis, the equipotential surfaces are planes normal to X-axis, i.e., planes parallel to YZ-plane.

Potential energy of a single charge in an external electric field:

Let a charge q is located at point P. The electric potential at point P is V. The potential energy of charge is given by the expression given below:

P.E. = q.V

Potential energy of a system of two charges in an external electric field:

Let two charges q1 and q2 are located at points M and N. Let r12 be radius vector from M to N. Let V1 and V2 be electric potentials at points M and N respectively. Potential energy of this sytem is given by the following expression :

P.E. = (q₁V₁) + (q₂V₂) + (k_Coulomb q₁ q₂ / r₁₂)

where, k_Coulomb = Coulomb's constant = 8.99 × 10⁹ N.m²/C².

Potential energy of a dipole in an external electric field:

Let a dipole be placed in an external electric field E. Let p be the dipole moment of this dipole. Let an external torque is applied on this dipole and it is rotated slowly from θ₀ to θ. The amount of work done in doing so is stored in this dipole as its potential energy and it is given by the expression :

P.E. = p E (cos θ₀ - cos θ)

Relation between work, charge, and potential:

Relation between work, charge, and electric potential is given by the following expression :

work = charge × potential

volt or V:

SIU of electric potential is volt or V.

electron volt or eV:

1 electron volt or 1 eV is defined as the amount of energy gained by an electron when it is displaced from one point to another point whose potential is higher by one volt. OR 1 electron volt or 1 eV is the amount of kinetic energy gained by an electron when it is accelerated through a potential difference of one volt.

1eV = 1.602 × 10^-19 J

Electric flux:

Electric flux is defined as number of electric lines of force passing normally through a given area. Let electric field E is passing through area dS. Then dot product of

E and dS gives us electric flux dφ through area dS. The expression for electric flux dφ is given below:

dφ = E • dS

SIUnit of electric flux is V.m. Electric flux dφ is a scalar quantity. E and dS are vector quantities but their dot product (scalar product) yields a scalar. Direction of area vector dS is perpendicular to area dS. Total electric flux φ passing through area S can be obtained by integrating both sides of above given expression, as shown below:

φ = ∫ E • dS