Magnetic lines of force:

Pursuing the analogy between electricity and magnetism, concept of magnetic lines of force is proposed as analogous to electric lines of force. A magnetic line of foce begins from N-pole and ends at S-pole. Inside the magnet, magnetic line of force begins from S-pole and ends at N-pole.

Poles of magnet:

Every magnet has two poles : N-pole (North pole) and S-pole (South pole). An isolated N-pole or S-pole cannot exists. If a magnet is broken into two pieces then every piece possesses two poles (N-pole and S-pole). Magnetic poles are said to be fictitious or imaginary. But concept of magnetic poles is very useful in study of magnetism.

Poles of magnet:

Every magnet has two poles : N-pole (North pole) and S-pole (South pole). An isolated N-pole or S-pole cannot exists. If a magnet is broken into two pieces then every piece possesses two poles (N-pole and S-pole). Magnetic poles are said to be fictitious or imaginary. But concept of magnetic poles is very useful in study of magnetism.

Magnetic flux (φ):

Magnetic flux (φ) is defined as number of magnetic lines of force passing normally through a given area. SIUnit of magnetic flux is weber or Wb. Magnetic flux is given by the following expression:

φ = B • A

where φ = magnetic flux, B = magnetic flux density, A = area. φ is a scalar quantity, whereas B and A are vector quantities. Direction of A is nothing but normal to the area. The dot product (aka scalar product, "aka" means "also known as") of B and A yields scalar quantity φ.

Magnetic dipole:

A bar magnet (or simply, a magnet) is also called as magnetic dipole.

Axis of magnet:

A line passing through both the poles of magnet is called an axis of magnet.

Equator of magnet:

A plane passing through centre of the magnet and perpendicular to its axis is called equator of magnet.

Magnetic length (2 l):

The distance between the two poles of a magnet is called magnetic length (2 l). Also, notice:

magnetic length (2 l) = (5/6) × geometrical length of magnet.

Also, l (it is small L, and not one) is nothing but distance between any pole of magnet and centre of magnet.

Pole strength:

Pole strength is defined as the concentration of strength of magnetism at the poles. For north pole, it is ‘+m’ and for south pole, it is ‘–m.’ Its SIUnit is A.m (or ampere.metre).

Magnetic dipole moment (M):

The magnetic dipole moment M is defined as the product of its pole strength m and its magnetic length (2 l). Therefore, M = m 2 l. SIUnit of magnetic dipole moment is Am². M and 2 l are vector quantities, whereas m is a scalar quantity. The direction of M or 2 l is same, it is directed from south pole to north pole.

Equivalence between a magnetic dipole and a current carrying coil:

Notice the following points in this regard:

(a) A current carrying coil as well as a magnetic dipole produces magnetic field around them,

(b) the magnetic lines of force due to magnet and current carrying coil are similar,

(c) a magnetic dipole, when placed in an electric field of intensity E, is acted upon by a torque τ, given by:

τ = M B sin θ

a current carrying coil, when suspended in a magnetic flux density B, is also acted upon by a torque given by:

τ = n I A B sin θ

because of equivalence between these two torques, quantity M = n I A is called the magnetic moment of current carrying coil, here n = number of turns of wire in coil and A = area of coil, and θ = angle between area vector A and magnetic field B,

(d) the magnitude of magnetic induction B at a point along the axis of a short magnetic dipole is given by the expresison:

B_axis = (μ₀ / 4π) × (2 M / r³)

whereas, the magnitude of magnetic flux density B at a point on the axis at a large distance (r) from the centre of circular coil carrying current I is given by the expression:

B_axis = (μ₀ / 4π) × (2 n I A / r³)

Torque acting on a magnet in uniform magnetic induction:

Torque acting on a magnet placed in uniform magnetic field is given by the expression:

τ = M B sin θ

where M = dipole moment of magnet, B = magnetic flux density, θ = angle between axis of magnet and direction of B. In vector form this expression is given as follows:

τ = M × B

Geographic axis of earth:

A straight line around which earth spins.

Geograpic meridian of earth:

At a given place, it is vertial plane passing through the geographic north and south of the earth.

Geographic equator of earth:

It is a great circle on the surface of earth, in a plane perpendicular to the geographic axis.

Magnetic axis of earth:

It is a straight line passing through the magnetic poles of the earth. It is inclined to the earth’s geographic axis by nearly 11.3^o.

Magnetic meridian of earth:

At any place, it is a vertical plane passing through the magnetic north and south poles of the earth.

Magnetic equator of earth:

It is a great circle on the surface of the earth, in a plane perpendicular to teh magnetic axis. It happens to pass through India near Trivendrum.

Magnetic (or field) declination:

Magnetic meridian varies from geographic meridian by a certain angle. The angle between the magnetic meridian and the geographic meridian at a place is known as magnetic (or field) declination or variation at that place.

Angle of dip:

The angle between the earth’s magnetic field at a place and the horizontal is known as the angle of dip at that place. It is 0^o on the magnetic equator and 90^o at the magnetic poles of the earth. At other places, its value lies between 0^o and 90^o. It is also given by the following expression:

tan δ = B_V / B_H

where δ = angle of dip, B_V = vertical component of earth’s magnetic induction B, B_H = horizontal component of earth’s magnetic induction B. Also,

B² = (B_V)² + (B_H)²

Factors affecting strength of electromagnet:

Soft iron is highly suitable for making core of elec- tromagnet. The material used for core of electromagnet should have high value of saturation magnetization, low retentivity and low coercivity. Soft iron possesses these qualities.

Magnetic flux density due to a bar magnet at a point along the axis of a bar magnet:

Magnetic flux density B_axis due to a bar magnet at point P which lies along the axis of a bar magnet, is given by the following expression:

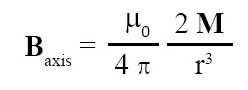
where B_axis = magnetic flux density due to a bar magnet at point P and point P lies along the axis of magnet, μ₀ = permeability of free space, r = OP = distance between centre of magnetic dipole O and point P, M = magnetic dipole moment. In this equation, B_axis and M are vector quantities.

Magnetic flux density at a point along the equator of a bar magnet:

Magnetic flux density B_equator at a point P which lies along the equator of a bar magnet is given by:

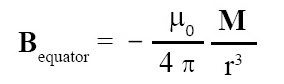
where, B_equator = magnetic flux density due to a bar magnet at point P and point P lies along the equator of magnet, μ₀ = permeability of free space, r = OP = distance between centre of magnetic dipole O and point P, M = magnetic dipole moment. In this expression B_equator and M are vector quantities.