Types of waves:

Waves are of three main types: (a) mechanical wave or elastic wave, (b) electromagnetic wave, and (c) matter wave.

Mechanical wave or elastic wave:

A wave which requires material medium for its propagation is called a mechanical wave or elastic wave. A mechanical wave exists only within a material medium such as water, air, metal, etc. Sound waves and waves on water surface are material waves. Sound waves are longitudinal waves and waves on water surface are transverse waves.

Electromagnetic wave:

Electric and magnetic disturbances travelling in vacuum with the speed of 3 lakh kilometer per second is called electromagnetic wave. Light waves, microwaves, x-rays, radio waves, and television waves are examples of electromagnetic waves. Electromagnetic waves are transverse waves.

Matter waves:

According to quantum physics, when a material particle moves, matter waves are associated with it. The wavelength of matter waves is given by the formula:

λ = h / p

where, λ = wavelength of matter waves, h = Planck’s constant = 6.62 × 10^-34 J.s, p = momentum of material particle.

Double periodicity:

Wave motion possesses double periodicity. It is periodic in space and also periodic in time.

Simple harmonic progressive wave:

The graphical representation of simple harmonic progressive wave is same as sine wave. The equation of simple harmonic progressive wave travelling in the direction of the positive x-axis, is given below:

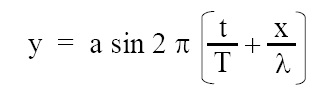
where, (x, y) = coordinates of an oscillating particle, t = time, T = time period of oscillation, λ = wavelength of wave.

Reflection of transverse wave:

If a transverse wave is incident on a rigid wall then crest is reflected back as trough and trough is reflected back as crest. Reflected wave then travels with opposite velocity and phase of wave changes by 180^o or π radian. If a transverse wave is incident on a wall made up of rarer medium then crest is reflected back as crest and trough is reflected back as trough. Reflected wave then travels with opposite velocity, however there is no change in phase.

Reflection of longitudinal wave:

If a longitudinal wave is incident on a rigid wall then compression is reflected back as compression and rarefaction is reflected back as rarefaction. Reflected wave then travels with opposite velocity and phase of wave changes by 180^o or π radian. If a longitudinal wave is incident on a wall made up of rarer medium then compression is reflected back as rarefaction and rarefaction is reflected back as compression. Reflected wave then travels with opposite velocity, however there is no change in phase.

Principle of superposition of waves:

When two or more waves travelling through a medium arrive at a point of the medium simultaneously, each wave produces its own displacement at that point independently of the others. Hence the resultant displacement at that point is equal to the vector sum of the displacements due to all the waves.

Constructive interference:

If two transverse waves meet at a point such that crest of first wave coincides with the crest of second wave and trough of first wave coincides with the trough of second wave then constructive interference takes place and a resultant wave with maximum amplitude is created. Similarly, if two longitudinal waves meet at a point such that compression of first wave coincides with the compression of second wave and rarefaction of first wave coincides with the rarefaction of second wave then constructive interference takes place and a resultant wave with maximum amplitude is created.

Destructive interference:

If two transverse waves meet at a point such that crest of first wave coincides with the trough of second wave and trough of first wave coincides with the crest of second wave then destructive interference takes place and a resultant wave with minimum amplitude is created. Similarly, if two longitudinal waves meet at a point such that compression of first wave coincides with the rarefaction of second wave and rarefaction of first wave coincides with the compression of second wave then destructive interference takes place and a resultant wave with minimum amplitude is created.

Beats:

If two sound notes (tuning forks) of slightly different frequencies (say, 510 Hz and 511 Hz) and equal amplitude are sounded together then we hear a sound note whose intensity is alternately maximum and minimum. This phenomenon is called beats. When sound becomes loud (maximum) we say sound is waxed and when sound becomes faint (minimum) we say sound is waned.

The alternate waxing and waning of sound after definite intervals of time due to superposition of two waves of nearly equal frequencies (say f₁ and f₂) is called beats. The number of times the sound waxes or wanes in one second is called frequncy of beats and it is given by following formula:

f = f₁ – f₂

where, f = frequnecy of beats, f₁ = frequency of one wave, f₂ = frequency of another wave. If f₁ = 511 Hz and f₂ = 510 Hz then f = 1 Hz.

Applications of beats:

(a) The phenomenon of beats is used to determine an unknown frequency. The sound note of known frequency is sounded together with sound note of unknown frequency, and then noting the frequency of beats, unknown frequency is computed.

(b) Musical instruments can be tuned by noting the beats produced when two different instruments are sounded together. The frequency of instrument to be tuned is adjusted till the frequency of beats is zero.

(c) Phenomenon of beats is used to produce low frequency notes used in Jazz orchestra or western music.

(d) Beats are used to detect the presence of dangerous gases in mines. Air sample collected from mine is blown through pipe or flute and clean air is blown through similar pipe or flute. Noting the difference between the sounds produced we can conclude about the presence of dangerous gases in air sample.

(e) Beats are also used for tuning the radio receivers.

Intensity of sound:

Intensity of sound is proportional to square of amplitude of sound wave.

Doppler effect for sound (Description):

When source of sound note and observer (listener) of sound note are in motion then frequency of sound note perceived by oberver (listener) can be different from the frequency of sound note generated by source.

Doppler effect for sound (Definition):

Doppler effect is the change in the frequency of sound wave observed by observer who is in relative motion with the source of sound. The observed frequency f is given by (it is assumed that motion of source and observer is restricted to one dimension):

f = [(v + v_observer) / (v – v_source)] x f₀

where f = frequency of sound observed by observer, v = speed of sound, vobserver = speed of observer, vsource = speed of source, f₀ = original frequency of sound emitted by source.

Depending upon the direction of observer and source, the values of v_observer and v_source can be positive or negative as follows:

(a) If observer is moving towards the source, then v_observer is positive. In this case, the numerator in the above given formula would stay same.

(b) If observer is moving away from the source, then v_observer is negative. In this case, the numerator in the above given formula would be replaced by (v – v_observer).

(c) If source of sound is moving towards the observer, then v_source is positive. In this case, the denominator in the above given formula would stay same.

(d) If source of sound is moving away from the observer, then v_source is negative. In this case, the denominator in the above given formula would be replaced by (v + v_source).

Doppler Effect for Light (for Stars, for frequencies):

The formula for Doppler effect for light (for stars), for frequencies, is given below:

f_observerd = f_source × [(1 + v/c) / (1 - v/c)]^1/2

where f_observerd = frequency of light observed by observer, f_source = frequency of light emitted by source of light, c = speed of light, v = speed of source of light. Here, v is positive when source is approaching the observer and v is negative if source is moving away from the observer. Also, notice that x^1/2 = square root of x.

The formula for ratio v/c - in Doppler effect for light - is given below:

k = f_observerd / f_source

v/c = (k² - 1) / (k² + 1)

where k = fobserverd / fsource, fobserverd = frequency of light observed by observer, fsource = frequency of light emitted by source of light, c = speed of light, v = speed of source of light. Here, v is positive when source is approaching the observer, and v is negative if source is moving away from the observer.

Doppler Effect for Light (for Stars, for wavelengths):

The formula for Doppler effect for light (for stars), for wavelengths, is given below:

λ_observed = λ_source × [(1 - v/c) / (1 + v/c)]^1/2

where λ_observerd = wavelength of light observed by observer, λ_source = wavelength of light emitted by source of light, c = speed of light, v = speed of source of light. Here, v is positive when source is approaching the observer and v is negative if source is moving away from the observer. Also, notice that x^1/2 = square root of x.

Applications of Doppler effect:

(a) In color Doppler sonography, the ultrasonic waves refracted from body tissues can give information about rate of flow of various fluids including blood.

(b) Traffic police use speed guns for detecting the speeds of vehicles on the road. The working of speed guns is based on the Doppler effect.

(c) The working of RADAR is based on Doppler effect. RADAR is used for detection of aeroplanes and it stands for RAdio Detection And Ranging of waves.

(d) Doppler effect can be used to determine the speed of a star.

(e) Doppler effect is used to determine the speed of rotation of the sun.