Stationary wave:

When two identical progressive waves both (transverse or longitudinal) travelling along the same path in opposite directions, interface with each other, by superposition of waves a resultant wave is obtained in the form of loops and is called a stationary wave or standing wave.

Equation of stationary wave:

Equation of stationary wave is given below:

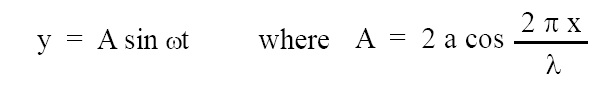
where, y = displacement of medium particle in resultant stationary wave, A = amplitude of resultant stationary wave, a = amplitude of individual interfering waves, λ = wavelength of resultant stationary wave as well as of individual interfering waves, ω = angular frequency of resultant stationary wave as well as of individual interfering waves, t = time, x = distance along x-axis. Here, individual interfering waves travel along x-axis in opposite directions. In the above equation, the terms ‘t’ and ‘x’ are not present in the same harmonic function hence it is not progressive wave but a stationary wave.

Antinodes:

The points of medium, which vibrate with maximum amplitude, are called antinodes. Antinodes are produced for x = 0, λ/2, λ, 3λ/2, The distance between any two successive antinodes is λ/2.

Nodes:

The points of medium, which vibrate with minimum amplitude, are called nodes. Nodes are produced for x = λ/4, 3λ/4, 5λ/4, ... The distance between any two successive nodes is λ/2. The distance between node and adjecent antinode is λ/4.

Properties of stationary waves:

(a) Two identical waves (both either transverse or longitudinal) travelling through a medium (along same path) in opposite directions, interfere with each other, produce resultant wave in the form of loops, is called stationary wave.

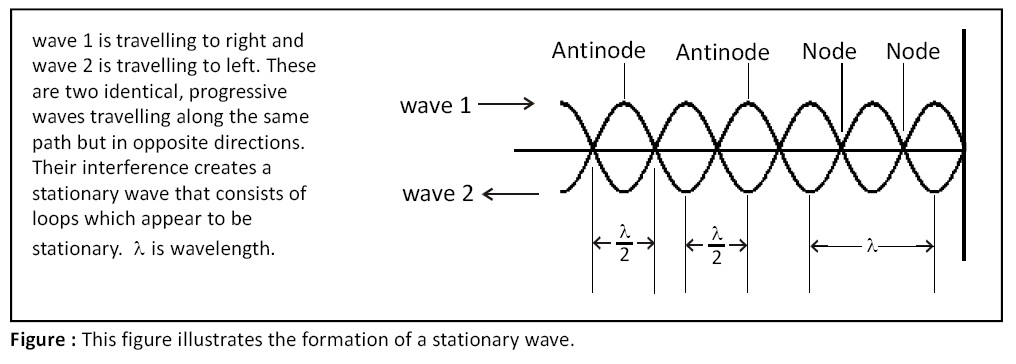
(b) In stationary wave, the points at which medium particles vibrate with minimum amplitude are called nodes, and the points at which medium particles vibrate with maximum amplitude are called antinodes.

(c) The distance between two successive nodes or antinodes is equal to half of wavelength (i.e., λ/2). Nodes and antinodes are equally spaced.

(d) In stationary wave, nodes and antinodes are alternately formed. The distance between node and adjecent antinode is quarter of wavelength (i.e., λ/4).

(e) In stationary wave, the particles of medium (except those at nodes) perform S.H.M. of the same period as that of component waves but of different amplitude.

(f) All the particles within the loop are in the same phase of vibration (or oscillation).

(g) The particles in adjacent loops are vibrating out of phase.

(h) Stationary wave is doubly periodic phenomenon (periodic in space and time).

(i) Stationary wave is standing wave, therefore the resultant velocity of the wave is zero. There is no transfer of energy through medium.

(j) In case of longitudinal stationary waves, the points at which displacement of particle is minimum but variation in pressure is maximum are called pressure antinodes and the points at which displacement of particle is maximum but variation in pressure is minimum, such points are called pressure nodes.

Speed of transverse wave in a string fixed at both ends:

The speed of transverse wave in a string fixed at both ends is given by following formula:

v = f λ = (T / m)^1/2

where, v = velocity of wave in string fixed at both ends, f = frequency of this wave, λ = wavelength of this wave, T = tension set up in the string, m = mass of string per unit length. Also, notice that x^1/2 means square root of x.

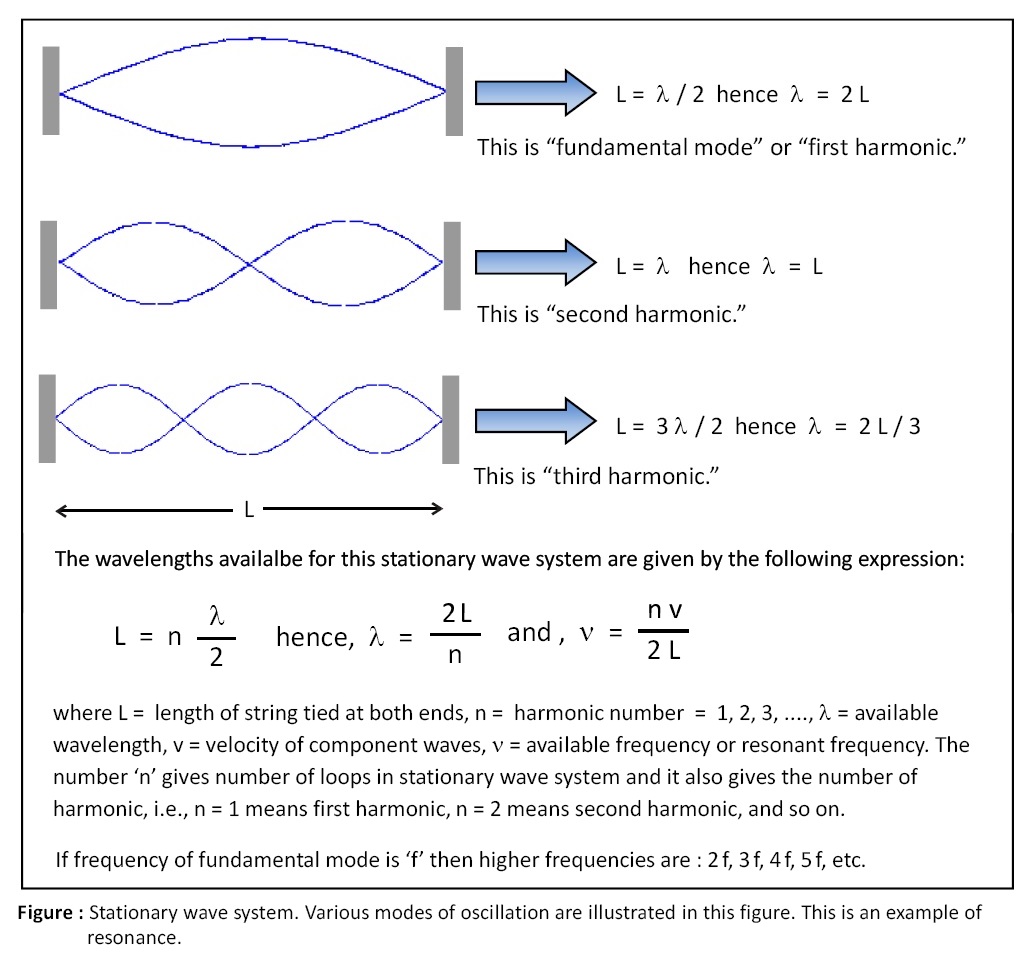
Normal modes:

In case of strings, the stationary wave pattern can be obtained by fixing it at both ends with some tension in it. However, this string cannot vibrate with any arbitrary frequency or wavelength, unlike a single harmonic wave travelling along a string which can have any frequency or wavelength. For example, a string of length L is tied at both ends to rigid walls then it can vibrate only in such a way that length of string should accomodate 1, 2, 3, ... loops. However, you cannot have a fractional number of loops in this system such as 2.5 or 3.7. Notice that length of a loop is always equal to λ/2. The set of available frequencies or resonant frequencies for stationary wave system is called normal modes.

Overtone:

In normal modes, if frequency of fundamental mode or first harmonic is ‘f’ then frequencies corresponding to higher harmonics are 2 f, 3 f, 4 f, 5 f, etc. These frequencies corresponding to higher harmonics (i.e., 2 f, 3f, 4 f, 5f, etc.) are called overtones. Notice that (p+1)^th harmonic is p^th overtone.

Relation between harmonic number ‘n’ and overtone number ‘p’:

Harmonic number ‘n’ is related to overtone number ‘p’ by the following expression :

n = p + 1

Frequency of fundamental mode or first harmonic:

The frequency of fundamental mode or first harmonic is given by the below given expression :

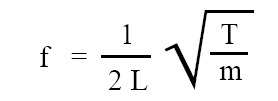
where, L = length of string, f = frequency of fundamental mode or first harmonic, T = tension set up in the string, m = mass per unit length of string.

Frequency of (p+1)^th harmonic or p^th overtone:

Frequency of (p+1)^th harmonic or p^th overtone is given by the following expression :

f_p = (p + 1) f = n f

where, f_p = frequency of p^th overtone or (p+1)^th harmonic, p = overtone number, n = harmonic number, f = frequency of fundamental mode or first harmonic.

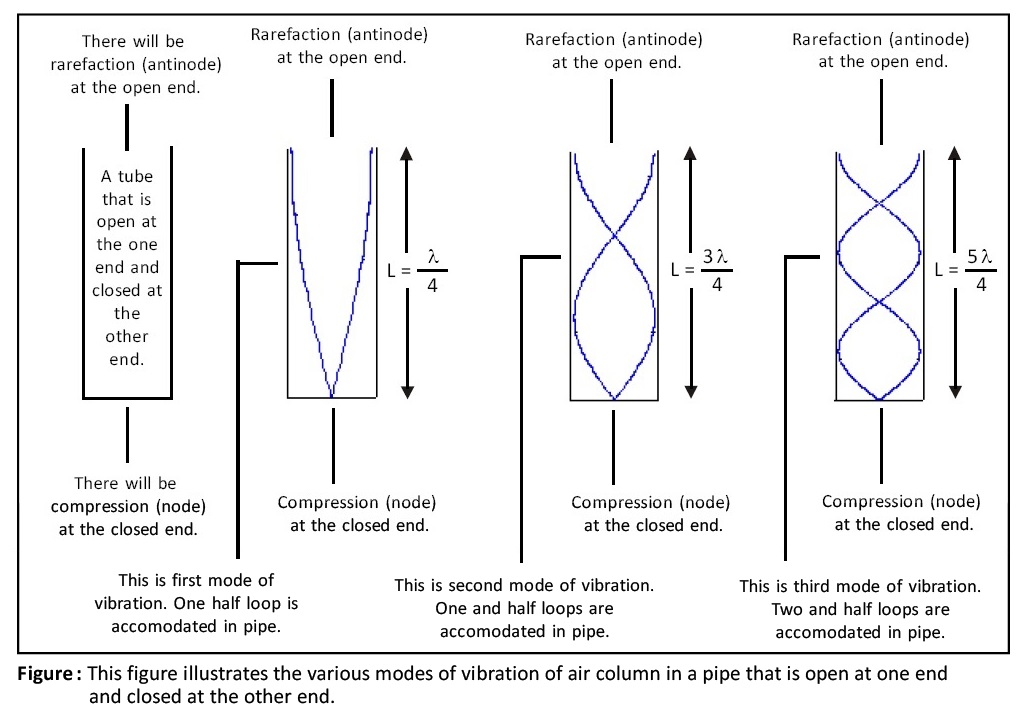
Modes of vibration of air column in a pipe closed at one end:

First three modes of vibration are shown in the below given figure.

The frequencies of vibration for first three modes are as follows:

First mode or fundamental mode of vibration:

The frequency of vibration for first mode or fundamental mode is given by the below given expression (see the below given figure):

f₁ = v / (4L)

where, f₁ = frequency of vibration for first mode or fundamental mode, v = velocity of sound, L = length of tube.

Second mode of vibration:

The frequency of vibration for second mode is given by the below given expression (see the below given figure):

f₂ = 3v / (4L)

where, f₂ = frequency of vibration for second mode, v = velocity of sound, L = length of tube.

Third mode of vibration:

The frequency of vibration for third mode is given by the below given expression (see the below given figure):

f₃ = 5v / (4L)

where, f₃ = frequency of vibration for third mode, v = velocity of sound, L = length of tube.

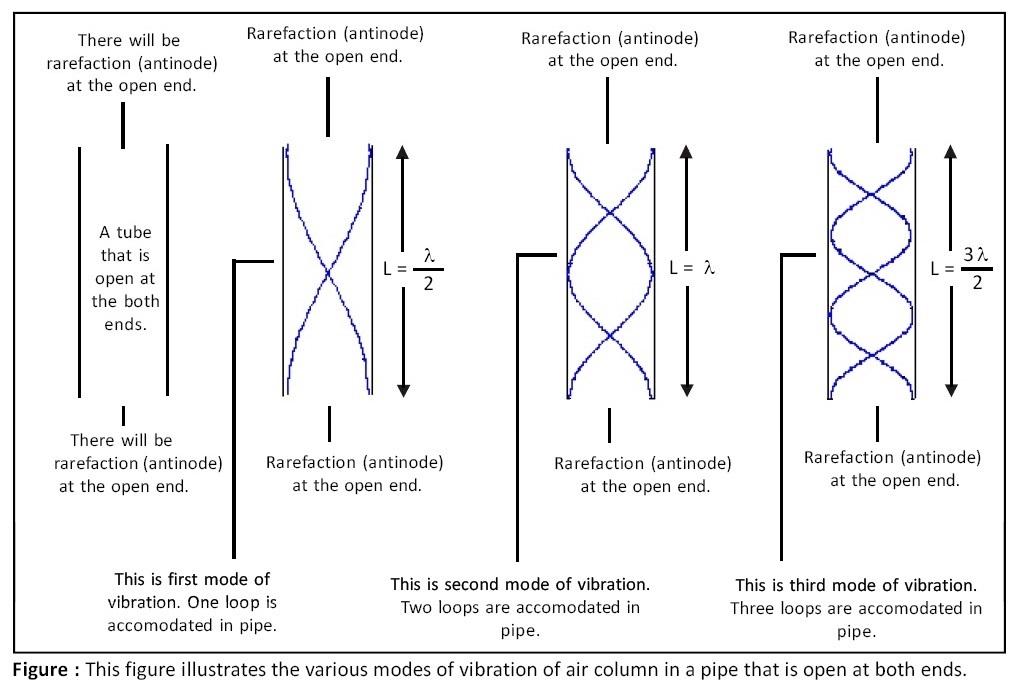
Modes of vibration of air column in a pipe open at both ends:

First three modes of vibration are shown in the below given figure. The frequencies of vibration for first three modes are as follows:

First mode or fundamental mode of vibration:

The frequency of vibration for first mode or fundamental mode is given by the below given expression (see the below given figure):

f₁ = v / (2L)

where, f₁ = frequency of vibration for first mode or fundamental mode, v = velocity of sound, L = length of tube.

Second mode of vibration:

The frequency of vibration for second mode is given by the below given expression (see the below given figure):

f₂ = v / L

where, f₂ = frequency of vibration for second mode, v = velocity of sound, L = length of tube.

Third mode of vibration:

The frequency of vibration for third mode is given by the below given expression (see the below given figure):

f₃ = 3v / (2L)

where, f₃ = frequency of vibration for third mode, v = velocity of sound, L = length of tube.

Free vibrations:

When a body, capable of oscillating, is displaced from its stable equilibrium position and released, it makes oscillations which are called free vibrations (or free oscillations) and the frequency of vibrations is called its natural frequency.

Forced vibrations:

The vibrations of body under action of external periodic force in which body vibrates with frequency equal to frequency of external periodic force (called driving frequency) other than its natural frequency are called forced vibrations.

Resonance:

Resonance is a special case of forced vibrations. The phenomenon in which the body vibrates under action of external periodic force, whose frequency is equal to the natural frequency of the driven body, so that amplitude becomes maximum is called resonance.

Examples of resonance:

(a) Standing wave pattern or stationary wave pattern shown in the three preceding figures are example of resonance.

(b) Sonometer, Melde’s experiment, and Helmoltz’s resonator are based on the principle of resonance.

Applications of resonance:

(a) Frequency of tuning fork can be found out by resonating it with tuning fork of known frequency.

(b) Radio receiver and television tune to desired station or channel because of resonance.

(c) Velocity of sound can be determined using pipe open at one end and closed at other end.

(d) Hollow wooden boxes are attached to musical instruments like satar, tambora, guitar, violin, etc. The volume resonance takes place inside these wooden boxes and louder sound is produced.

(e) Resonance is also used for the analysis of musical notes.

Disadvantages of resonance:

(a) If soldiers are marching on the bridge with disciplined footsteps, and if frequency of their footsteps matches with the frequency of natural vibration of bridge, then resonance occurs, bridge vibrates vigorously and collapses.

(b) In an auditorium, if frequency of clapping by audience matches with the frequency of natural vibration of roof of auditorium, then resonance occurs, roof vibrates vigorously and collapses.

(c) When speed of aircraft increases gradually, then different parts are forced to resonate and vibrate vigorously causing risk to flight.

(d) In a rough sea, if the natural frequency of swinging of ship matches with the frequency of water waves, then resonance occurs, ship vibrates vigorously, and may sink.

Types of musical instruments:

The musical instruments are classified into the four types: (a) stringed instruments, (b) wind instruments, (c) percussion instruments, and (d) solid instruments.

Stringed musical instrument:

Musical instrument in which sound is produced by plucking the strings, is called a stringed musical instrument. In sitar and tambora, strings are plucked by fingers. In piano, strings are plucked by hammer.

Wind musical instrument:

Musical instrument in which sound is produced by setting vibration of air column is called wind musical instrument. Examples: flute, bugle, bassoon, and harmonium.

Percussion musical instrument:

Musical instrument in which sound is produced by setting vibrations in a stretched membrane is called a percussion musical instrument. Examples, tabala, dholak, halagi, and drum.